Задание 1. Даны матрицы
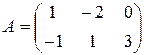 ,
, 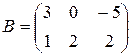 ,
, 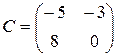 .
.
Найти матрицы а) 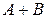 , б)
, б) 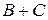 , в)
, в) 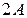 , г)
, г) 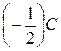 , д)
, д) 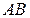 , е)
, е) 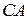 если они существуют.
если они существуют.
Решение:
а) Матрицы А и В одинаковых размеров  , поэтому находим по правилу сложения
, поэтому находим по правилу сложения
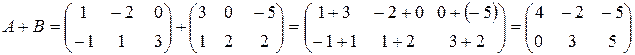 .
.
б) Матрица В имеет размеры  , а матрица С -
, а матрица С - 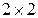 . Поскольку размеры матриц не совпадают, операцию сложения выполнить нельзя.
. Поскольку размеры матриц не совпадают, операцию сложения выполнить нельзя. 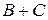 не существует.
не существует.
в) По правилу произведения матрицы на число находим:
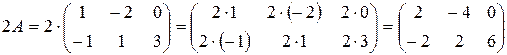 .
.
г) По правилу произведения матрицы на число находим:
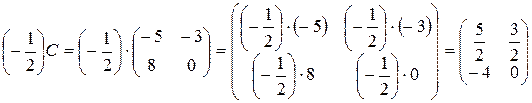 .
.
д) Поскольку матрица А имеет размеры  , а матрица В -
, а матрица В -  , то матрица
, то матрица 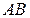 не существует
не существует
Поскольку матрица С, имеет размеры 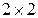 , а матрица А -
, а матрица А - 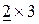 , то матрица
, то матрица 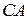 существует и по правилу умножения матриц находим:
существует и по правилу умножения матриц находим:
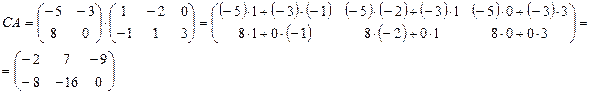
Задание 2. Даны матрицы
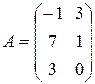 ,
, 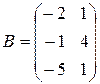 ,
, 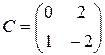 .
.
Найти матрицы а) 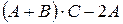 , б)
, б) 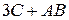 .
.
Решение:
а) Шаг 1: определить порядок выполнения операций над матрицами: сначала выполняется транспонирование матриц, затем выполняется действие в скобках, затем операции умножения, затем сложения.
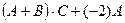
Шаг 2: последовательно выполнить все операции, установив предварительно, что размеры матриц позволяют это сделать.
1) Матрицы А и В одинаковых размеров, поэтому можно найти
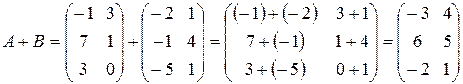 .
.
2) Матрица 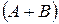 имеет размеры
имеет размеры 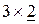 , матрица С имеет размеры
, матрица С имеет размеры 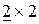 , поэтому можно найти
, поэтому можно найти
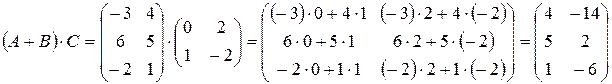 .
.
3) 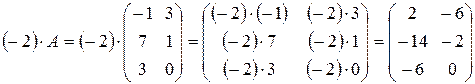 .
.
4) Матрицы 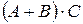 и
и 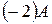 имеют одинаковые размеры, поэтому можно найти
имеют одинаковые размеры, поэтому можно найти
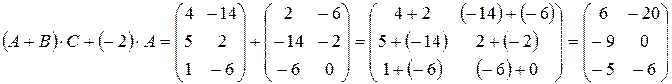
б) Шаг 1: Определить порядок выполнения операции
Шаг 2: Вторая операция 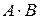 недопустима, т.к. размеры матрицы А -
недопустима, т.к. размеры матрицы А - 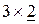 и размеры матрицы В -
и размеры матрицы В - 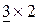 . Следовательно, матрица
. Следовательно, матрица 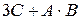 не существует.
не существует.
 2015-05-10
2015-05-10 315
315








