Задание 1. Вычислить определитель матрицы:
а) 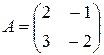 , б)
, б) 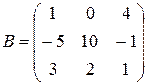 , в)
, в) 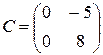 , г)
, г) 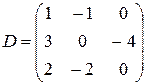 .
.
Решение:
а) Матрица A второго порядка, поэтому определитель находим по формуле (2):
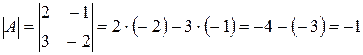 .
.
б) Матрица B третьего порядка, поэтому определитель находим по формуле (3):
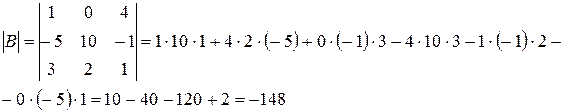
в) Матрица C содержит столбец, состоящий из нулей, поэтому по свойству 1): 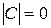 .
.
г) Матрица D содержит 2 строки (1-я и 3-я) с пропорциональными элементами, поэтому по свойству 3): 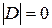 .
.
Задание 2. Решить систему уравнений по формулам Крамера:
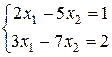 .
.
Решение:
Шаг 1: найти определитель системы
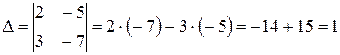 .
.
Т.к. 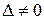 , то по теореме Крамера система имеет единственное решение
, то по теореме Крамера система имеет единственное решение
Шаг 2: вычислить определители 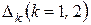 :
:
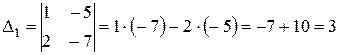 .
.
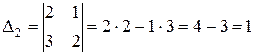 .
.
Шаг 3: по формулам Крамера (5) найти решение системы
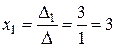 ,
, 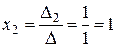 .
.
Шаг 4: сделать проверку, подставив полученные значения переменных в систему уравнений:
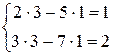 ,
, 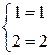 .
.
 2015-05-10
2015-05-10 332
332








