Задание 1. Найти матрицу, обратную матрице
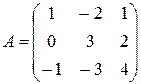 .
.
Решение:
Шаг 1. Вычислим определитель матрицы A:
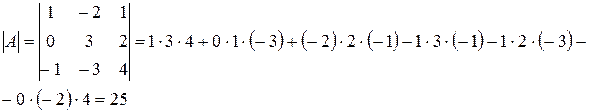
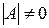 , следовательно по теореме (3) существует
, следовательно по теореме (3) существует 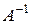 .
.
Шаг 2. Составим прямоугольную матрицу 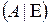 :
:
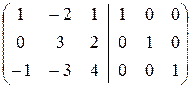
Шаг 3. С помощью строчечных элементарных преобразований приведем матрицу 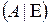 к виду
к виду 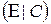 :
:
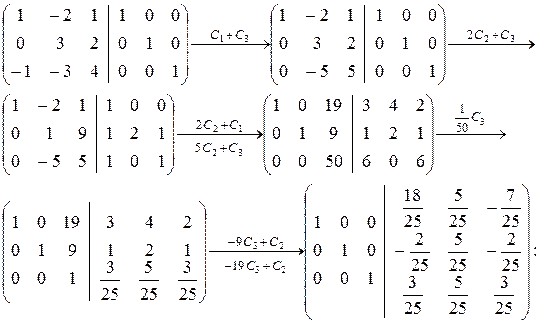
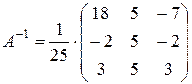 .
.
Шаг 4. Сделаем проверку:
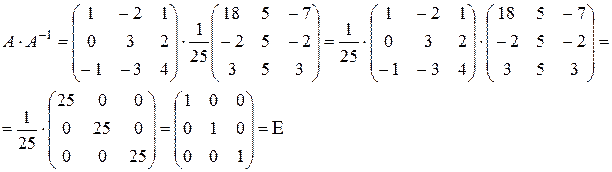 .
.
Задание 2. Решить матричным способом систему уравнений:
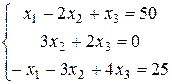 .
.
Решение:
Шаг 1. Записать систему уравнений в виде матричного уравнения 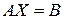 , где
, где
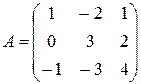 ,
, 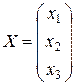 ,
, 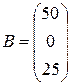 .
.
Шаг 2. Так как 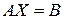
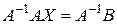
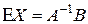
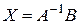 ,
,
то для того чтобы найти решение системы уравнений 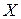 , достаточно найти обратную матрицу
, достаточно найти обратную матрицу 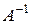 . Используя решение предыдущего задания, получаем:
. Используя решение предыдущего задания, получаем:
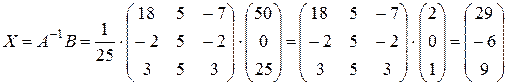 .
.
Т.о., 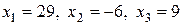
Шаг 3. Сделаем проверку: 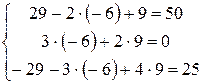 .
.
Равенства верны, следовательно получено верное решение системы уравнений: 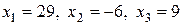 .
.
 2015-05-10
2015-05-10 488
488








