Краткие теоретические сведения. Квадратичная матрица называется единичной, если все ее элементы, расположенные вдоль главной диагонали равны единице

Квадратичная матрица 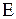называется единичной, если все ее элементы, расположенные вдоль главной диагонали равны единице, а остальные элементы равны нулю:

.

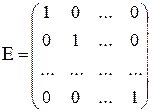Если квадратные матрицы A и 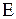одного порядка, то .

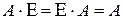Матрица 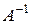называется обратной по отношению к квадратной матрице A, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

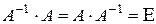(2)

Матрица A называется невырожденной, если ее определитель отличен от нуля: .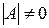

Теорема. Обратная матрица 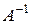существует (и единственна) тогда и только тогда, когда исходная матрица A невырожденная.

Над строками матрицы можно выполнять строчные элементарные преобразования (аналогично преобразованиям уравнений линейной системы):

1) Перестановка местами двух строк матрицы;

2) Прибавление к любой строке матрицы другой ее строки, умноженное на произвольное число;

3) Удаление нулевой строки матрицы;

4) Умножение всех элементов строки матрицы на число не равное нулю.

Алгоритм нахождения обратной матрицы .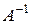

Шаг 1. Используя результат теоремы, установить существует или нет обратная матрица 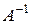. Если существует, перейти к следующему шагу.

Шаг 2. Составить прямоугольную матрицу 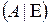, где A - исходная квадратная матрица, 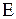- единичная матрица размеров как у A.

Шаг 3. С помощью строчных элементарных преобразований привести матрицу 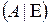к виду 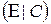. Полученная при этом матрица C является матрицей .

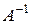Шаг 4. Сделать проверку – убедиться, что выполняется равенство (2).