Шаг 1. С помощью строчечных элементарных преобразований привести расширенную матрицу (3) системы линейных уравнений (1) к ступенчатому виду:
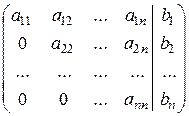
Шаг 2. Если в ступенчатой матрице присутствует строка вида (0, 0, …, 0| b), где 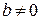 , то системе уравнений (1) не имеет решений. В противном случае перейти к следующему шагу.
, то системе уравнений (1) не имеет решений. В противном случае перейти к следующему шагу.
Шаг 3. Если в ступенчатой матрице присутствуют нулевые строки вида (0, 0, …, 0| 0), то следует их удалить.
Шаг 4. Если число строк r в ступенчатой матрице меньше числа неизвестных 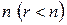 , то системе (1) имеет бесконечное число решений, переходим к шагу 5. Если
, то системе (1) имеет бесконечное число решений, переходим к шагу 5. Если 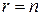 , то системе (1) имеет единственное решение, переходим к шагу 6.
, то системе (1) имеет единственное решение, переходим к шагу 6.
Шаг 5. Составить систему уравнений, соответствующих ступенчатой матрице. Выразить любые r неизвестных системы через остальные неизвестные и свободные члены это общее решение системы (1).
Шаг 6. Составить систему равнений, соответствующих ступенчатой матрице. Последовательно «снизу вверх» выразить неизвестные системы. Т.о. будет получено ее единственное решение.
Шаг 7. Сделать проверку: подставить решение в систему уравнений.
 2015-05-10
2015-05-10 609
609








