2015-05-10
371
Задание 1. Решить систему уравнений методом Гаусса:
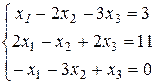
Решение:
Шаг 1. Приведем расширенную матрицу системы к ступенчатому виду:
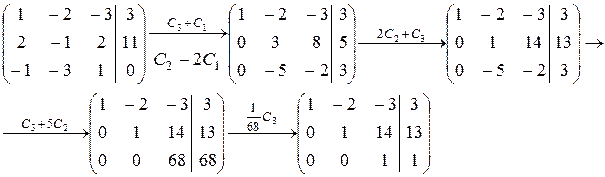
Шаг 2. Система (1) совместная, т.к. ступенчатая матрица не имеет строк вида
(0, 0, …, 0| b).
Шаг 3. Нулевых строк ступенчатая матрица не содержит.
Шаг 4. Число строк ступенчатой матрицы равно числу неизвестных системы уравнений: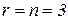 
. Следовательно система имеет единственное решение.
Шаг 6. Составим систему уравнений, соответствующую ступенчатой матрице и выполним ее решение «снизу вверх»:
.
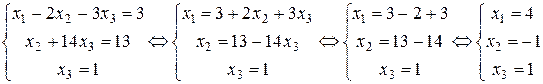Шаг 7. Сделаем проверку:
.
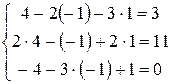Получили верное равенство, следовательно система уравнений решена верно.
Задание 2. Решить систему уравнений методом Гаусса:
.
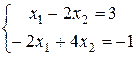Решение:
Шаг 1. Приведем расширенную матрицу системы к ступенчатому виду:
.
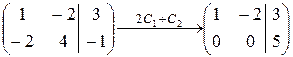Шаг 2. Т.к. ступенчатая матрица содержит строку (0, 0, 15), система уравнений не имеет решений.
Задание 3. Решить систему уравнений методом Гаусса:
.
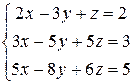Решение:
Шаг 1. Приведем расширенную матрицу системы к ступенчатому виду:
.
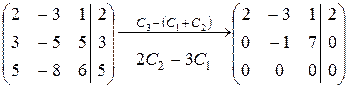Шаг 2. Система уравнений совместна, т.к. ступенчатая матрица не содержит строк вида (0, 0, …, 0| b)..
Шаг 3. Удалим нулевую строку
.
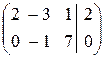Шаг 4. Т.к. число строк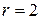 
в ступенчатой матрице меньше числа неизвестных 
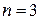, то система имеет бесконечное множество решений.
Шаг 5. По полученной матрице составим систему уравнений и выразим первые две переменные через третью переменную:
.
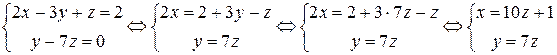Общее решение системы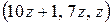 
, где z - любое число. Для получения частного рения положим, например, z= 1. Частное решение имеет вид (11, 7, 1).
