Теория и расчет

Отношение между угловым моментом 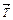твердого тела в неподвижной системе координат и началом в центре тяжести с моментом 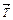, действующим на него, имеет вид:

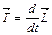(1)

Угловой момент выражается из угловой скорости 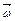и тензора моментов инерции из

.

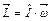В данном случае 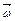направлена в сторону главной оси инерции (оси z), поэтому у 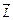только один компонент:

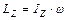
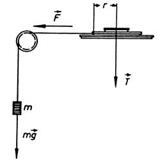
Рис. 2: Момент силы на вращательной плоскости.

где 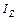- компонент 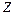главного тензора момента инерции тела. Отсюда выражение (1) преобразуется в

.

Момент силы 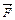(см. рис. 2)

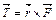
при 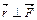равен

.

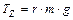Таким образом, уравнение движения имеет вид:

.

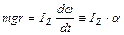Далее получаем

.

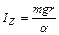Момент инерции 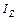тела с плотностью 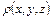равен

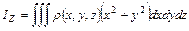
а) для плоского диска радиусом 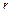и массой 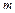получаем

.

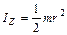На основе имеющихся характеристик диска

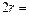0,350 м

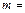0,829 кг

получаем

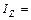12,69·10^-3 кг·м².

Среднее значение измерянных моментов инерции составляет

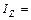12,71·10^-3 кг·м².

б) Для длинного стержня массой 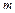и длиной 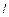получаем

.

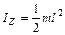На основе имеющихся характеристик диска

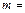0,158 кг

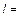0,730 м

получаем

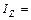7,017·10^-3 кг·м².

Среднее значение измерянных моментов инерции составляет

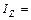6,988·10^-3 кг·м².

в) для материальной точки с массой 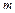на расстоянии 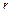от оси вращения получаем

.

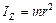Для проведения измерений было выбрано расстояние 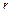= 0,15 м.

Из графика функции на рис. 3:

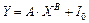
(где 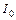- момент инерции стержня), получаем экспоненту

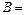1,00±0,02 (см (2)).

Измерения проводились при массе 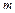= 0,2 кг.

Из графика на рис. 4 функции получаем экспоненту

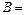1,93±0,03 (см (2)).

Рис. 3: Зависимость момента инерции материальной точки от массы.

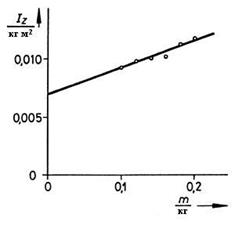
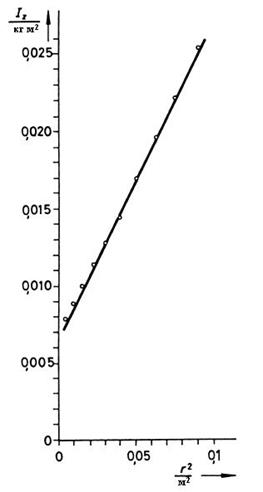
Рис. 4: Зависимость момента инерции материальной точки от квадрата расстояния от оси вращения.