Закон распределения полностью задает случайную величину. Однако, часто этот закон неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам.
Пусть некоторая дискретная случайная величина 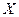 задана законом распределения
задана законом распределения
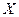
| 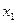
| 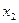
| 
| 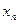
|
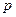
| 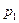
| 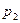
| 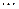
| 
|
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на соответствующие вероятности:
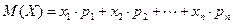 .
.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины 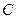 равно этой величине:
равно этой величине:
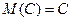 .
.
2. Постоянный множитель можно выносить за знак математического ожидания:
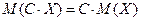 .
.
3. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
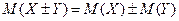 .
.
4. Математическое ожидание произведения независимых величин равно произведению их математических ожиданий:
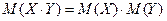 .
.
Дисперсией 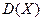 дискретной случайной величины
дискретной случайной величины 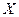 называют математическое ожидание квадрата отклонения случайной величины
называют математическое ожидание квадрата отклонения случайной величины 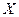 от ее математического ожидания:
от ее математического ожидания:
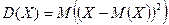 .
.
Дисперсия характеризует рассеяние возможных значений случайной величины относительно ее математического ожидания.
Свойства дисперсии дискретной случайной величины
1. Дисперсия дискретной случайной величины 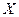 равна разности между математическим ожиданием квадрата величины
равна разности между математическим ожиданием квадрата величины 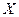 и квадратом ее математического ожидания:
и квадратом ее математического ожидания:
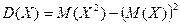
2. Дисперсия постоянной величины равна нулю.
3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
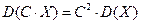 .
.
4. Дисперсия суммы (разности) независимых случайных величин равна сумме их дисперсий:
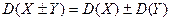 .
.
Средним квадратическим отклонением 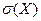 случайной величины
случайной величины 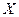 называют корень из ее дисперсии:
называют корень из ее дисперсии:
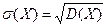 .
.
Пример 8. Вычислить числовые характеристики дискретной случайной величины X, заданной законом распределения.
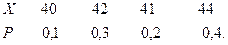
Решение. Для вычисления 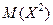 составим следующий закон распределения величины
составим следующий закон распределения величины 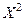 :
:
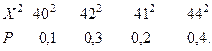
Тогда
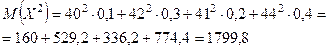
и 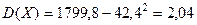
3) Для характеристики рассеяния возможных значений случайной величины вокруг ее среднего значения вводится среднее квадратическое отклонение 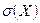 случайной величины Х, равное квадратному корню из дисперсии
случайной величины Х, равное квадратному корню из дисперсии 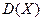 , то есть
, то есть
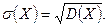
Из этой формулы имеем: 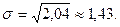
 2015-05-12
2015-05-12 489
489








