Группа
02. Сколькими способами можно переставить буквы в слове АРБУЗ?
Группа
12. Кафедра физвоспитания приобрела для футбольной команды 16 футболок с номерами от 1 до 16. Игроки наудачу берут 10 футболок. Найти вероятность того, что футболка под номером 13 окажется не взятой..
Группа
22. Ящик содержит 90 годных и 10 дефектных деталей. Сборщик последовательно достает из ящика 10 деталей. Найти вероятность того, что среди взятых деталей хотя бы одна дефектная.
Группа
32. В каждой из трех коробок содержится 9 белых и 7 зеленых шаров. Из первой коробки наудачу взят один шар и переложен во вторую коробку, после чего из второй коробки извлечен один шар и переложен в третью коробку. Найти вероятность того, что шар, наудачу извлеченный из третьей коробки, окажется зеленым.
Группа
42. В роддоме родилось 12 детей. Найти вероятность того, что среди них 7 мальчиков. Вероятность рождения мальчика 0,51.
.
Группа
52. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.
Группа
62. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
| X | 4,3 | 5,1 | 10,6 |
| p | 0,2 | 0,3 | 0,5 |
Группа
Случайная величина Х задана интегральной функцией распределения F(x). Найти: 1) дифференциальную функцию распределения f(x); 2) математическое ожидание M(Х); 3) дисперсию D(Х); 4) среднеквадратическое отклонение σ(Х); 5) построить графики функций F(x), f(x).
72. 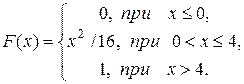 |
Группа
82. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):
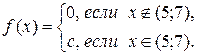
Группа
Выборка задана в виде распределения частот. а) Найти распределение
относительных частот. б) Найти эмпирическую функцию по данному распределению выборки и построить график функции F(x).
92.
|
Группа
102. Построить полигон относительных частот по данному распределению выборки:
| xi | |||||
| wi | 0,1 | 0,2 | 0,1 | 0,25 | 0,35 |
Группа
112. Найти выборочную среднюю по данному распределению выборки объема n=15:
| xi | |||
| ni |
Группа
122. Из генеральной совокупности извлечена выборка объема n=10:
| xi | ||||
| ni |
Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
Группа
Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии Y на X.
132.
| X | ||||||||||
| Y |
Группа
Найти основные выборочные характеристики 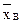 , s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ для следующей выборки:
, s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ для следующей выборки:
| Номер задачи | |
| 142. | |
| 12,6 18,7 15,3 14,8 19,5 13,7 16,4 15,2 16,3 12,9 18,5 16,5 15,4 13,6 16,9 15,8 17,3 19,6 15,8 19,6 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется испытанием, событием? Приведите примеры испытаний, событий.
2. Какие события называются достоверными, невозможными, случайными. Приведите примеры этих событий.
3. Какие события называются несовместными, совместными? Приведите примеры.
4. Какие события называются противоположными? Приведите примеры.
5. Сформулируйте классическое определение вероятности. Укажите возможные границы вероятности.
6. Что понимается под суммой двух событий? Приведите примеры.
7. Сформулируйте теорему сложения вероятностей для несовместных событий.
8. Какие события называют независимыми, зависимыми? Приведите примеры.
9. Что понимается под произведением двух событий? Приведите примеры.
10. Сформулируйте теоремы умножения вероятностей для независимых и зависимых событий.
11. Сформулируйте теорему сложения вероятностей для совместных событий.
12. Что понимается под полной группой событий? Чему равна сумма вероятностей событий, составляющих полную группу?
13. Приведите формулу полной вероятности, формулу Байеса. При каких условиях они применяются?
14. Приведите формулу Бернулли. При решении какого типа задач она применяется?
15. Сформулируйте локальную теорему Лапласа. При каких условиях она применяются?
16. Сформулируйте интегральную теорему Лапласа.
17. Приведите формулу Пуассона. При каких условиях она применяются?
18. Какие случайные величины называются дискретными? непрерывными? Приведите примеры.
19. Что называется законом распределения дискретной случайной величины? Как он задается?
20. Что называется многоугольником распределения дискретной случайной величины?
21. Дайте определение математического ожидания дискретной случайной величины.
22. Перечислите основные свойства математического ожидания.
23. Дайте определение дисперсии и среднего квадратического отклонения дискретной случайной величины.
24. Перечислите свойства дисперсии.
25. Дайте определение интегральной функции распределения. Перечислите ее свойства.
26. Дайте определение дифференциальной функции распределения. Перечислите ее свойства.
27. Как вычисляются числовые характеристики непрерывной случайной величины.
28. Какое распределение дискретной случайной величины называется биномиальным?
29. Чему равны числовые характеристики случайной величины, распределенной по биномиальному закону?
30. Какое распределение непрерывной случайной величины называется равномерным? Какой параметр характеризует равномерное распределение и как найти его значение?
31. Какое распределение непрерывной случайной величины называется нормальным? Какие параметры характеризуют нормальное распределение?
32. Начертите кривую нормального распределения. Как меняется кривая при изменении параметров нормального распределения?
33. Перечислите свойства нормального распределения.
34. Сформулируйте правило трех сигм.
35. Что понимается под генеральной совокупностью?
36. Что такое выборка? Что называется вариантами выборки и вариационным рядом?
37. Что такое частота появления варианты в выборке?
38. Как получают относительную частоту появления варианты в выборке?
39. Как построить полигоны частот и относительных частот?
40. Как построить гистограммы частот и относительных частот?
41. В чем сущность задачи по определению параметров генеральной совокупности?
42. Какую величину принимают за среднюю генеральной совокупности? Как она вычисляется?
43. Какую величину принимают за дисперсию генеральной совокупности? Как она вычисляется?
44. Как вычисляется среднее квадратическое отклонение средней выборки?
45. Что понимают под доверительным интервалом и доверительной вероятностью?
46. Как вычислить доверительный интервал для математического ожидания нормально распределенной случайной величины в случае, когда среднее квадратическое отклонение известно; когда среднее квадратическое неизвестно?
47. Дайте определение корреляционной зависимости.
48. В чем состоят две основные задачи теории корреляции?
49. Какую корреляционную зависимость называют линейной?
50. Дайте определение выборочного коэффициента корреляции и перечислите его свойства.
51. Что можно сказать о зависимости двух случайных величин, если коэффициент корреляции rВ = 0, rВ = 1, rВ = –1?
52. Запишите выборочные уравнения прямых регрессий.
Приложение 1
Таблица значений функции 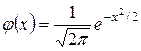
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,3989 0,2420 0,0540 0,0044 |
Приложение 2
Таблица значений функции 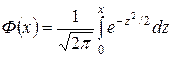
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | |||||||
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 | 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753 0,0793 0,0832 0,0871 0,0910 0,0948 | 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 | 0,0987 0,1026 0,1064 0,1103 0,1141 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879 | 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 | 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549 0,2580 0,2611 0,2642 0,2673 0,2703 | 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 | 0,2734 0,2764 0,2794 0,2823 0,2852 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389 | |||||||
| 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 | 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830 0,3849 0,3869 0,3883 0,3907 0,3925 0,3944 0,3962 0,3980 | 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 | 0,3997 0,4015 0, 4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 | 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 1,80 1,81 1,82 1,83 | 0,4406 0,4418 0,4429 0,4441 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4525 0,4633 0,4641 0,4649 0,4656 0,4664 | 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 2,16 2,18 2,20 2,22 | 0, 4671 0, 4678 0,4686 0,4693 0,4699 0,4706 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 0,4846 0,4854 0,4861 0,4868 | |||||||
| 2,24 2,26 2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42 2,44 2,46 | 0,4875 0,4881 0,4887 0,4893 0,4898 0,4904 0,4909 0,4913 0,4918 0,4922 0,4927 0,4931 | 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 2,68 2,70 | 0, 4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961 0,4963 0,4965 | 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 | 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981 0,4982 0,4984 | 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00 | 0,4985 0,4986 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0, 499997 | |||||||
Приложение 3
Таблица значений tγ = t (γ, n)
| γ n | 0,95 | 0,99 | 0,999 | γ n | 0,95 | 0,99 | 0,999 |
| 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 | 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 | 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 | ∞ | 2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960 | 2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576 | 3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291 |
Приложение 4
Таблица значений q = q (γ, n)
| γ n | 0,95 | 0,99 | 0,999 | γ n | 0,95 | 0,99 | 0,999 |
| 1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39 | 2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60 | 5,64 3,88 2,98 2,42 2,06 1,80 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60 | 0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089 | 0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120 | 0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162 |
1. Андронов А.М., Копытов Е.А., Гринглаз Л.Я. Теория вероятностей и математическая статистика. – Москва: Питер, 2004.- 464с.
2. Бочаров П.П., Печенкин А.В. Теория вероятностей: Учеб. пособие. – М.: Изд–во ун–та Дружбы народов, 1994.
3. Беляев Ю.К., Носко В.П. Основные понятия и задачи математической статистики. – М.: Изд–во МГУ, ЧеРо, 1998.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. – Изд. 6–е доп. – М.: Высш.шк., 2002.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для студентов вузов. Изд. 6–е, доп. – М.: Высш. шк., 2002.
6. Гнеденко Б.В. Курс теории вероятностей: Учебник. – М.: Наука, 1988.
7. Крамер Г. Математические методы статистики. – М.: Госиноиздат, 1948.
8. Мешалкин Л.Д. Сборник задач по теории вероятностей. – М.: Изд–во МГУ, 1963.
9. Теория вероятностей. Методическое пособие. – Рига: TSI, 2002. – 75с.
 2015-05-12
2015-05-12 1877
1877







