И.Е.Тамм и модель Кронига-Пенни

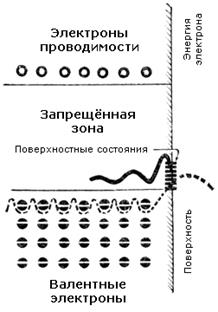
Рис. 5. Схема энергетических состояний в кристалле, ограниченном поверхностью

В безграничной кристаллической решетке спектр энергии электрона состоит из чередующихся непрерывных полос или зон, которые разделены «запрещенными» участками. Размытие энергетических уровней отдельных атомов в непрерывные зоны связано с коллективизацией электронов в решетке: при объединении атомов в кристалл электроны начинают переходить от одного атома к другому, и энергетический спектр такого делокализованного электрона в пределах разрешенной зоны близок к непрерывному. «Полосатая» структура спектра с необходимостью вытекает из периодичности в расположении атомов кристалла – дальнего порядка. Если кристалл ограничен поверхностью, то периодичность решетки нарушается (по крайней мере, а направлении, перпендикулярном к поверхности). При этом оказываются разрешенными и такие значения энергии, которые попадают в запрещенные зоны. Это и есть таммовские поверхностные уровни. Электрон в таммовском состоянии напоминает поплавок на поверхности воды: он может свободно двигаться вдоль поверхности, но не способен ни уйти в глубь твердого тела, ни выйти из тела наружу. Электроны как бы прилипают к поверхности. Такое поведение электронов в поверхностных состояниях описывается волновой функцией (жирная кривая), экспоненциально спадающей в глубь кристалла. Пунктирная кривая изображает потенциальную энергию электрона в кристалле. Из хода этой кривой видно, что для того, чтобы оказаться в вакууме, электрону необходимо преодолеть потенциальный барьер. Для простоты на рисунке не показан изгиб зон вблизи поверхности.

И.Е.Тамм предположил, что в случае полубесконечного кристалла ход межатомного микроскопического потенциала в одномерной модели (а он использовал модель Кронига-Пенни) можно представить, как показано на рис.6. В этом случае ход потенциала переодичен внутри кристалла при х > 0, а за его пределами при х < 0 он становиться постоянным U (х) = U_s = Const.

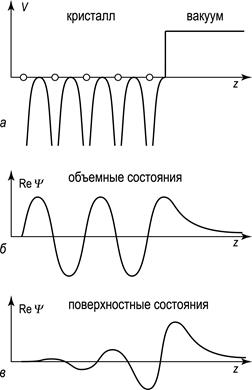
Рис.6.

Тогда решение одномерного уравнения Шредингера можно искать во всем интервале изменения х (-∞ до + ∞) при условии непрерывности и конечности волновой функции и ее производной, ее периодичности и ограниченности в объеме кристалла. Решение уравнения Шредингера (1) должно иметь вид, аналогичный (3).

Ψ_кр= А₁U_к(х)е^ikx + А₂U_-к(х)е^-ikx (9),

Где А₁, А₂ – постоянные; U_к(х), U_-к(х) - периодические функции с периодом постоянной рещетки (а=с); К(Е) - функция энергии электрона, которая в случае бесконечного кристалла, как было показано выше, может иметь только вещественные значения.

В случае полубесконечного кристалла для Е < U_s в области х < 0 появляется возможное (ограничено при х → ∞) решение:

Ψ_вак = Аехр {(2m (U_s – Е))^1/22πх/h} (10).

Условие сшивки двух пространственно ограниченных решений при х = 0 дает два линейных уравнения для нахождения трех коэффициентов А₁, А₂, А.

Ψ_кр = Ψ_вак А₁U_к(0) + А₂U_-к(0) = А

Ψ_кр^/ = Ψ_вак^/ А₁ [Uк^/(0) +ikUк^/(0)] + А₂ [U_-к^/(0) - ik U_-к(0)] =

А{(2m (U_s – Е))^1/22π/h} (11)

Помимо этой системы уравнений выбор коэффициентов А_1, А₂, А ограничен только условиями конечности волновой функции в объеме кристалла.

Возможны два случая:

1. К(Е) – вещественно, т.е. значение энергии электрона лежит в разрешенных зонах кристалла. В этом случае волновая функция в объеме кристалла ограничена, а система представляет собой два уравнения для трех неизвестных, т.е. не накладывает дополнительных условий на выбор коэффициентов. Это означает, что в ограниченном кристалле разрешенными являются все энергетические уровни, разрешенные в бесконечном кристалле.

2. К(Е) – комплексно (значение энергии электрона соответствует запрещенным зонам кристалла). В этом случае необходимость конечности волновой функции в объеме кристалла обязывает положить равным нулю либо А₁, либо А₂ (в зависимости от знака мнимой части К). Пусть А₂ = 0. Тогда система уравнений (11) представляет собой два уравнения для двух неизвестных и, следовательно, имеет решение только в случае равенства нулю детерминанта. Таким образом, в ограниченном кристалле возможны разрешенные дискретные значения энергии электрона в области энергий, соответствующих запрещенным зонам кристалла.

Пусть К = πn/a + iμ, тогда для волновой функции поверхностных состояний (ПС) можно записать:

Ψ_ss= А₁U_к(х)е^inπ/a е^-μx x > 0

Ψ_ss= А exp {(2m (U_s – Е))^1/22πх/h} x < 0 (12)

Волновая функция монотонно затухает по мере удаления от поверхности в вакуум и осциллируя затухает в глубь кристалла. В этом случае уравнение (7) – условие равенства нулю дитерминанта системы линейных уравнений для объема кристалла примет вид:

(-1)ⁿ chμa = P/αa * Sinαa + Cosαa (13),

Т.е. Е = Е(U₀,μ,а₀).

Условие равенства нулю дитерминаната системы (11) примет вид:

(-1)ⁿ exp (-μa) = {(2m (U_s – Е))^1/22πa/h}*Sinαa + Cosαa (14),

Т.е. Е = Е(U_s,μ,а).

Уравнения (13) и (14) дают нам систему из двух транцендентных уравнений для определения собственных значений энергии Е_n и волнового квантового числа μ_n (k_n = nπ/a + i μ_n) для электрона на ПС.

Анализ нетривиального решения этой системы уравнений показал, что при условии Е < U_s в каждом интервале запрещенных энергий nπ < αa < (n+1)π имеется по одному разрешенному значению Е_n и соответствующему ему μ_n > 0 только при условии:

4πmaU₀b/h² = P > 4πa²(2m U_s)/h² , т.е. U₀b > 2aU_s. Здесь U₀b – характеризует потенциальную энергию взаимодействия валентного электрона с атомным остатком, aU_s – потенциальную энергию взаимодействия электрона вблизи поверхности кристалла со всем полем в нем.

Таммовские ПС возникают вследствие нарушения периодичности внутреннего микропотенциала на поверхности полубесконечного кристалла.

Концентрация таммовских ПС равна поверхностной концентрации атомов в кристалле, т.е. величине порядка 10¹⁵ см^-2. При такой высокой концентрации состояний в поверхностной зоне, если эта зона заполнена частично, возможно появление металлической проводимости вдоль поверхности кристалла.

Поверхностные состояния образуются не только на границе между твердым телом и вакуумом. Поверхность раздела может быть внутренней, например, разграничивающей два разных полупроводниковых кристалла. Такую поверхность стали называть гетеропереходом, а пару разделяемых ею полупроводников – гетероструктурой. На внутренней поверхности раздела в гетероструктуре электрон может быть заперт с двух сторон брэгговскими отражениями, если его энергия попадает одновременно в запрещенные зоны обоих кристаллов.