Вычисление объема выпускаемой продукции и температуры.
В табл. 16 приведены данные, полученные в результате эксперимента, целью которого являлось определение тесноты связи между объемом выпуска продукции и температурой определенного технологического процесса.
1. Построить диаграмму рассеяния(корреляционное поле) для этой совокупности данных.
2. Оценить тесноту связи между объемом выпуска продукции и температурой.
Таблица 16
Данные по объему продукции и температуры процесса
Температура 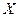 | |||||||||||
Объем выпуска продукци  , шт , шт |
1.Если мы построим корреляционное поле, то замечаем, что существует сильная нелинейнуя взаимосвязь, для которой характерен незначительный случайный разброс.
Коэффициент парной корреляции, 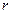 =-0,0155, бесполезен в случае такой нелинейной связи: с его помощью невозможно решить, является связь увеличивающей или уменьшающей, поскольку в действительности есть и то и другое. В этом случае целесообразно использовать корреляционное поле, поскольку оно демонстрирует, что для максимального увеличения объема выпускаемой продукции температуру производственного процесса следует установить равной примерно 700 "С. Объем продукции резко падает как при слишком высокой, так и при слишком низкой температуре. Этот важный вывод можно сделать, наблюдая на диаграмме сильную взаимосвязь между объемом продукции и температурой.
=-0,0155, бесполезен в случае такой нелинейной связи: с его помощью невозможно решить, является связь увеличивающей или уменьшающей, поскольку в действительности есть и то и другое. В этом случае целесообразно использовать корреляционное поле, поскольку оно демонстрирует, что для максимального увеличения объема выпускаемой продукции температуру производственного процесса следует установить равной примерно 700 "С. Объем продукции резко падает как при слишком высокой, так и при слишком низкой температуре. Этот важный вывод можно сделать, наблюдая на диаграмме сильную взаимосвязь между объемом продукции и температурой.
(Замечание. Близкое к нулю значение коэффициента корреляции может означать как отсутствие взаимосвязи в данных, так и наличие нелинейной взаимосвязи без преобладания направленности вниз или вверх. Сильная нелинейная взаимосвязь может быть даже тогда, когда корреляция близка к нулю!)
2. Оценим тесноту связи между объемом выпуска продукции и температурой с помощью корреляционного отношения. Значения результативного признака  разобьем на пять групп, т.е.
разобьем на пять групп, т.е. 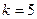 (табл. 17). В основу группировки кладется исследуемый фактор
(табл. 17). В основу группировки кладется исследуемый фактор 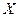 .
.
Таблица 17
Таблица группированных данных
| Номер группы | Количество элементов в 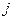 -й группе, -й группе, 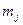 | Значения 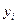 , попавшие в , попавшие в 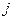 -ю группу -ю группу | Среднее значение  в в 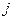 -й группе, -й группе, 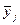 | 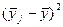 |
| 127; 139 | 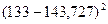 | |||
| 147; 147 | 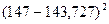 | |||
| 155; 154; 153 | 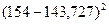 | |||
| 148; 146 | 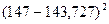 | |||
| 136; 139 | 132,5 | 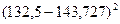 |
Вычислим общую среднюю 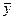 , используя средние значения в каждой группе
, используя средние значения в каждой группе
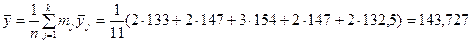 .
.
Найдем межгрупповую дисперсию:
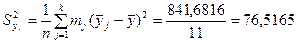 .
.
Вычислим общую дисперсию:
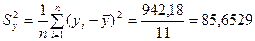 .
.
Получим корреляционное отношение
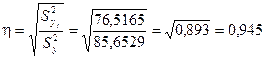 .
.
Значение 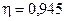 свидетельствует о наличии сильного нелинейного влияния температуры на объем выпуска продукции.
свидетельствует о наличии сильного нелинейного влияния температуры на объем выпуска продукции.
4. Регрессионный анализ. Основная задача регрессионного анализа заключается в исследовании зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели.
В регрессионных моделях зависимая (объясняемая) переменная  может быть представлена в виде функции
может быть представлена в виде функции 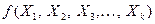 , где
, где 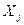 ,
, 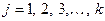 . – независимые (объясняющие) переменные, или факторы. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность предприятия или курс ценной бумаги. В зависимости от вида функции
. – независимые (объясняющие) переменные, или факторы. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность предприятия или курс ценной бумаги. В зависимости от вида функции 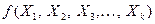 модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов
модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов 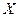 модели делятся на однофакторные (парная модель регрессии) и многофакторны е (модель множественной регрессии).
модели делятся на однофакторные (парная модель регрессии) и многофакторны е (модель множественной регрессии).
Связь между переменной  и
и 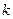 независимыми факторами можно охарактеризовать функцией регрессии
независимыми факторами можно охарактеризовать функцией регрессии 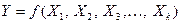 , которая показывает, каково будет в среднем значение переменной
, которая показывает, каково будет в среднем значение переменной  , если переменные
, если переменные 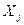 примут конкретные значения.
примут конкретные значения.
Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений.
Сформулируем регрессионную задачу для случая однофакторного признака.
Пусть имеется набор значений двух переменных: 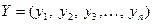 – объясняемая переменная и
– объясняемая переменная и 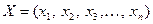 – объясняющая переменная, каждая из которых содержит
– объясняющая переменная, каждая из которых содержит 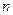 наблюдений. Для того чтобы правильно выбрать тип регрессионного уравнения, следует знать условный закон распределения зависимой переменной
наблюдений. Для того чтобы правильно выбрать тип регрессионного уравнения, следует знать условный закон распределения зависимой переменной  . На основе графика не всегда удается определить его однозначно, поэтому строят несколько регрессионных моделей, а затем по определенным критериям определяют лучшую модель. Если в проводимом исследовании можно ограничиться построением линейной модели, выбирают ее. Такая популярность и предпочтительность объясняется тем, что математический аппарат для линейных моделей хорошо разработан, а сами модели легко интерпретируемы. Пусть между переменными
. На основе графика не всегда удается определить его однозначно, поэтому строят несколько регрессионных моделей, а затем по определенным критериям определяют лучшую модель. Если в проводимом исследовании можно ограничиться построением линейной модели, выбирают ее. Такая популярность и предпочтительность объясняется тем, что математический аппарат для линейных моделей хорошо разработан, а сами модели легко интерпретируемы. Пусть между переменными 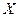 и
и  теоретически существует некоторая линейная зависимость
теоретически существует некоторая линейная зависимость
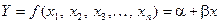 .
.
Это уравнение будем называть «истинным» уравнением регрессии.
Однако в действительности между 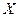 и
и  наблюдается не столь жесткая связь. Отдельные наблюдения
наблюдается не столь жесткая связь. Отдельные наблюдения 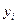 будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и неизвестных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде
будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и неизвестных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде
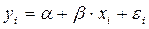 ,(3.6)
,(3.6)
где 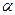 - постоянная величина (или свободный член уравнения),
- постоянная величина (или свободный член уравнения), 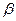 - коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений,
- коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений, 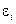 – случайная переменная (случайная составляющая, остаток, возмущение). Коэффициент
– случайная переменная (случайная составляющая, остаток, возмущение). Коэффициент 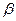 характеризует изменение переменной
характеризует изменение переменной 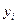 , при изменении значения
, при изменении значения 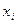 на единицу. Если
на единицу. Если 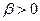 - переменные
- переменные 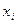 и
и 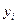 положительно коррелированные, если
положительно коррелированные, если 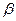 < 0 – отрицательно коррелированны;
< 0 – отрицательно коррелированны; 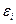 – независимые одинаково распределенные случайные величины – остаток с нулевым математическим ожиданием (
– независимые одинаково распределенные случайные величины – остаток с нулевым математическим ожиданием (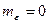 ) и постоянной дисперсией (
) и постоянной дисперсией (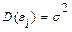 ). Она отражает тот факт, что изменение
). Она отражает тот факт, что изменение 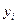 будет неточно описываться изменением
будет неточно описываться изменением 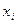 , так как присутствуют другие факторы, неучтенные в данной модели. Таким образом, в данном уравнении значение каждого наблюдения
, так как присутствуют другие факторы, неучтенные в данной модели. Таким образом, в данном уравнении значение каждого наблюдения 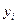 представлено как сумма двух частей – систематической
представлено как сумма двух частей – систематической 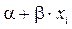 и случайной
и случайной 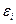 . В свою очередь, систематическую часть можно представить в виде уравнения
. В свою очередь, систематическую часть можно представить в виде уравнения 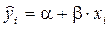 . Можно сказать, что общим моментом для любой регрессионной модели является разбиение зависимой переменной на две части – объясненную и случайную. Рассчитанные значения
. Можно сказать, что общим моментом для любой регрессионной модели является разбиение зависимой переменной на две части – объясненную и случайную. Рассчитанные значения 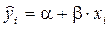 называются теоретическими (выравнеными) значениями
называются теоретическими (выравнеными) значениями 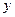 .
.
 2015-05-13
2015-05-13 1142
1142
