Имеется информация, содержащая проранжированные данные о годовых выплатах руководителям финансовых компаний (табл.10).
Таблица 10
Данные о годовых выплатах руководителям компаний
| № региона | Среднегодовая численность занятых, тыс. чел. х1 | № региона | Среднегодовая численность занятых, тыс. чел. х1 |
| 87,7 | 941,3 | ||
| 104,8 | 1044,2 | ||
| 246,6 | 1104,6 | ||
| 328,6 | 1129,5 | ||
| 390,8 | 1173,4 | ||
| 396,6 | 1229,8 | ||
| 483,3 | 1313,1 | ||
| 488,6 | 1333,8 | ||
| 598,3 | 1427,8 | ||
| 606,3 | 1586,8 | ||
| 678,2 | 1755,1 | ||
| 706,1 | 1795,3 | ||
| 766,0 | 1846,2 |
Требуется определить, имеются ли в наборе данных резко выделяющиеся значения. Определим ранг нижнего квартиля: 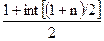 =
= 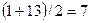 , соответствующее ему значение – 483,3 тыс. чел. Ранг верхнего квартиля:
, соответствующее ему значение – 483,3 тыс. чел. Ранг верхнего квартиля:  – ранг нижнего квартиля = 26 + 1 – 7 = 20, соответствующее ему значение – 1313,1 тыс. чел.
– ранг нижнего квартиля = 26 + 1 – 7 = 20, соответствующее ему значение – 1313,1 тыс. чел.
Для оценки выбросов определим, имеется ли среднегодовая численность занятых, превышающая величину: верхний квартиль + 1,5(верхний квартиль – нижний квартиль) = 1313,1 + 1,5(1313,1 – 483,3) = 2557,8 тыс. чел. Среднегодовая численность, величина которой меньше, чем: нижний квартиль – 1,5 (верхний квартиль – нижний квартиль) = 483,3 – 1,5(1313,1 –483,3) = –761,4, – в исследуемой совокупности не встречается.
Основными средствами анализа данных являются парные коэффициенты корреляции, частные коэффициенты корреляции и множественные коэффициенты корреляции.
При изучении взаимосвязи между двумя факторами их, как правило, обозначают
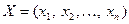 и
и 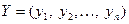 .
.
Ковариация – это статистическая мера взаимодействия двух переменных. Например, положительное значение ковариации доходности двух ценных бумаг показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону.
Ковариация между двумя переменными 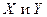 рассчитывается следующим образом:
рассчитывается следующим образом:
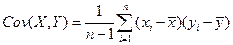 ,
,
где 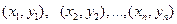 - фактические значения случайных переменных x и y,
- фактические значения случайных переменных x и y,
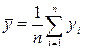 ,
, 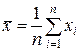 .
.
Ковариация зависит от единиц, в которых измеряются переменные  . Поэтому для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции.
. Поэтому для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции.
Для двух переменных  коэффициент парной корреляции определяется следующим образом:
коэффициент парной корреляции определяется следующим образом:
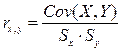 =
= 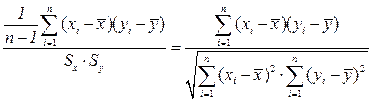 ,
,
где 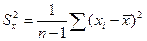
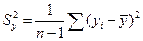 - оценки дисперсий величин
- оценки дисперсий величин 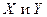 .
.
Эти оценки характеризуют степень разброса значений 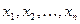
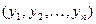 вокруг своего среднего
вокруг своего среднего 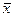 (
(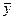 соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений.
соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений.
Слагаемые в числителе формулы, определяющей коэффициент парной корреляции, выражают взаимодействие двух переменных и определяют знак корреляции (положительная или отрицательная). Если, например, между переменными существует сильная положительная взаимосвязь (увеличение одной переменной при увеличении второй), каждое слагаемое будет положительным числом. Аналогично, если между переменными существует сильная отрицательная взаимосвязь, все слагаемые в числителе будут отрицательными числами, что в результате дает отрицательное значение корреляции.
Знаменатель выражения для коэффициента парной корреляции просто нормирует числитель таким образом, что коэффициент корреляции оказывается легко интерпретируемым числом, не имеющим размерности, и принимает значения от -1 до +1.
Числитель выражения для коэффициента корреляции, который трудно интерпретировать из-за необычных единиц измерения, есть ковариация X и Y. Несмотря на то что иногда она используется как самостоятельная характеристика (например, в теории финансов для описания совместного изменения курсов акций на двух биржах), удобнее пользоваться коэффициентом корреляции. Корреляция и ковариация представляют, по сути, одну и ту же информацию, однако корреляция представляет эту информацию в более удобной форме.
Следует отметить, что величина коэффициента корреляции не является доказательством того, что между исследуемыми признаками существует причинно-следственная связь, а представляет собой оценку степени взаимной согласованности в изменениях признаков. Для того чтобы установить причинно-следственную зависимость, необходим анализ качественной природы явлений.
Так как оценка тесноты связи с помощью коэффициента корреляции проводится, как правило, на основе более или менее ограниченной информации об изучаемом явлении, то возникает вопрос: насколько правомерно наше заключение по выборочным данным о наличии корреляционной связи в той генеральной совокупности, из которой была извлечена выборка?
В связи с этим и возникает необходимость оценки существенности (значимости) линейного коэффициента корреляции, дающая возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляции.
Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием 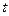 -критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерия определяется по формуле
-критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерия определяется по формуле
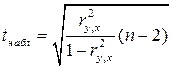
Вычисленное по этой формуле значение tнабл сравнивается с критическим значением 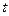 -критерия, которое берется из таблицы значений
-критерия, которое берется из таблицы значений 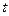 -критерия Стьюдента с учетом заданного уровня значимости и числа степеней свободы.
-критерия Стьюдента с учетом заданного уровня значимости и числа степеней свободы.
Если 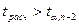 , где
, где 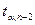 - табличное значение критерия Стьюдента, определенное на уровне значимости
- табличное значение критерия Стьюдента, определенное на уровне значимости 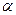 при числе степеней свободы
при числе степеней свободы 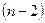 , то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
, то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Доверительный интервал (интервальная оценка) значимого коэффициента корреляции: 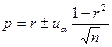 . Здесь
. Здесь 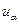 - критическая точка стандартного нормального распределения, соответствующая уровню значимости
- критическая точка стандартного нормального распределения, соответствующая уровню значимости 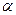 ;
; 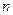 - объем выборки.
- объем выборки.
Если значение 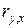 близко к нулю, связь между переменными слабая. Если корреляция между случайными величинами:
близко к нулю, связь между переменными слабая. Если корреляция между случайными величинами:
· положительная, то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать;
· отрицательная, то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
На практике для вычислений коэффициента корреляции часто используют следующую формулу:
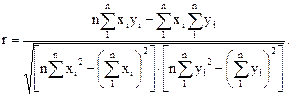
Коэффициент корреляции можно рассчитать и по другой формуле:
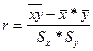 ,
,
где
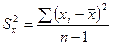 и
и 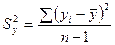 .
.
Используя данные табл. 6.4, рассчитаем значение r.
Таблица 11
Расчетные данные для оценки коэффициента корреляции
| № региона | уi | хi | xi∙yi | хi ² | уi ² | |
| 505717,3 | 1846,2 | 933655279,3 | 3408454,44 | 255749987519,3 | ||
| 42521,1 | 328,6 | 13972433,46 | 107977,96 | 1808043945,2 | ||
| 56735,9 | 396,6 | 22501457,94 | 157291,56 | 3218962348,8 | ||
| 605575,2 | 1795,3 | 3223102,09 | 366721322855,0 | |||
| 163001,5 | 26569489002,3 | |||||
| 91847,3 | 598,3 | 54952239,59 | 357962,89 | 8435926517,3 | ||
| 393319,4 | 1333,8 | 524609415,7 | 1779022,44 | 154700150416,4 | ||
| 96404,8 | 706,1 | 68071429,28 | 498577,21 | 9293885463,0 | ||
| 380921,3 | 1755,1 | 668554973,6 | 3080376,01 | 145101036793,7 | ||
| 299683,5 | 1044,2 | 312929510,7 | 1090353,64 | 89810200172,3 | ||
| 91074,5 | 678,2 | 61766725,9 | 459955,24 | 8294564550,3 | ||
| 490197,5 | 1586,8 | 2517934,24 | 240293589006,3 | |||
| 1173,4 | 235529541,6 | 1376867,56 | 40290124176,0 | |||
| 101314,1 | 606,3 | 61426738,83 | 367599,69 | 10264546858,8 | ||
| 11147,8 | 87,7 | 977662,06 | 7691,29 | 124273444,8 | ||
| 90555,4 | 390,8 | 35389050,32 | 152724,64 | 8200280469,2 | ||
| 14820,4 | 104,8 | 1553177,92 | 10983,04 | 219644256,2 | ||
| 51027,5 | 246,6 | 12583381,5 | 60811,56 | 2603805756,3 | ||
| 167894,4 | 1104,6 | 185456154,2 | 1220141,16 | 28188529551,4 | ||
| 585879,2 | 1427,8 | 836518321,8 | 2038612,84 | 343254436992,6 | ||
| 323307,4 | 1129,5 | 365175708,3 | 1275770,25 | 104527674894,8 | ||
| 337409,1 | 1313,1 | 443051889,2 | 1724231,61 | 113844900762,8 | ||
| 286888,6 | 1229,8 | 352815600,3 | 1512408,04 | 82305068810,0 | ||
| 247539,4 | 941,3 | 233008837,2 | 886045,69 | 61275754552,4 | ||
| 186506,9 | 488,6 | 91127271,34 | 238729,96 | 34784823747,6 | ||
| 87649,2 | 483,3 | 42360858,36 | 233578,89 | 7682382260,6 | ||
| Итого | 5909662,7 | 23562,8 | 28373959,94 | 2147563405123,1 | ||
| Средняя величина | 227294,7 | 906,3 | 290303129,1 | 1091306,152 | 82598592504,7 |
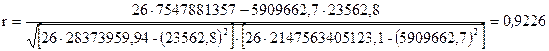
Напомним, что величина r изменяется от –1 до +1. Чем ближе по абсолютной величине коэффициент корреляции к нулю, тем связь меньше, и наоборот, чем ближе по абсолютной величине коэффициент корреляции к единице, тем связь сильнее. В пределе, когда коэффициент корреляции обращается в единицу, связь становится функциональной. Если с увеличением факторного признака х результативный признак у имеет тенденцию к увеличению, то r находится от 0 до 1, если с увеличением х величина у уменьшается, то r может принимать значения от –1 до 0.
Полученная величина коэффициента корреляции r = 0,92 свидетельствует о наличии достаточно тесной прямой зависимости между рассматриваемыми признаками.
Квадрат коэффициента корреляции носит название коэффициента детерминации: 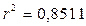 , то есть 85,11% вариации объема валового регионального продукта, объясняется вариацией среднегодовой численности занятых.
, то есть 85,11% вариации объема валового регионального продукта, объясняется вариацией среднегодовой численности занятых.
Следующий этап корреляционного анализа связан с расчетом множественного (совокупного) коэффициента корреляции.
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других переменных, рассматриваемых в корреляционном анализе.
Пусть имеется совокупность случайных переменных 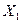 ,
, 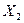 , …,
, …, 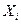 , …,
, …, 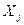 , …,
, …, 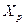 , имеющих совместное нормальное распределение. Матрица Q
, имеющих совместное нормальное распределение. Матрица Q
составленная из парных коэффициентов корреляции 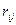 , где
, где 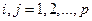 , называется корреляционной. Теснота линейной взаимосвязи одной переменной
, называется корреляционной. Теснота линейной взаимосвязи одной переменной 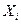 с совокупностью других (р - 1) переменных, рассматриваемой в целом, измеряется с помощью коэффициента множественной корреляц ии
с совокупностью других (р - 1) переменных, рассматриваемой в целом, измеряется с помощью коэффициента множественной корреляц ии 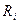 (i=l, 2, …, p):
(i=l, 2, …, p): 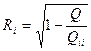 , где Q - определитель корреляционной матрицы,
, где Q - определитель корреляционной матрицы, 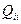 - алгебраическое дополнение корреляционной матрицы,
- алгебраическое дополнение корреляционной матрицы,  .
.
Если изучается связь между результативным признаком  и лишь двумя факторными признаками
и лишь двумя факторными признаками 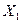 и
и 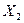 , то для вычисления множественного коэффициента корреляции можно использовать следующую формулу
, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу
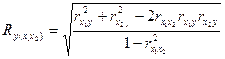 ,
,
где 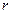 - парные коэффициенты корреляции.
- парные коэффициенты корреляции.
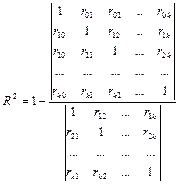 ,
,
где rij — парные коэффициенты корреляции между регрессорами 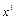 и
и 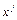 , a ri0 — парные коэффициенты корреляции между регрессором
, a ri0 — парные коэффициенты корреляции между регрессором 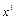 и y;
и y;
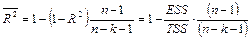 — скорректированный (нормированный) коэффициент детерминации.
— скорректированный (нормированный) коэффициент детерминации.
Нулевая гипотеза H0:b i = 0.
Альтернативная гипотеза H1: bI ¹ 0.
t-статистика имеет вид:
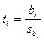 ,
,
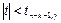 — область принятия нулевой гипотезы.
— область принятия нулевой гипотезы.
Если выполняется данное условие, то принимается нулевая гипотеза, и регрессор xi признается незначимым. В противном случае принимается альтернативная гипотеза, и регрессор признаётся значимым.
F-тест (тест Фишера) на значимость всей регрессии.
Нулевая гипотеза H0 :R2 = 0.
Альтернативная гипотеза H1:R2 ¹ 0.
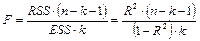 ,
,
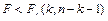 — область принятия нулевой гипотезы.
— область принятия нулевой гипотезы.
Если выполняется данное условие, то принимается нулевая гипотеза, и вся регрессионная модель признается незначимой. В противном случае принимается альтернативная гипотеза, и модель признаётся значимой.
Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества m признаков n наблюдений получают матрицу коэффициентов парной корреляции R.
Пусть вся совокупность данных состоит из переменной 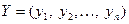 и
и 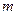 переменных факторов
переменных факторов 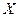 , каждая из которых содержит
, каждая из которых содержит 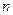 наблюдений. Значения переменных
наблюдений. Значения переменных  и
и 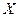 , содержащиеся в наблюдаемой совокупности, записываются в таблицу 12.
, содержащиеся в наблюдаемой совокупности, записываются в таблицу 12.
Таблица 12
| Переменные Номер наблюдения |  | 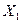 | 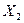 |  | 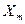 |
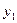 | 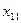 | 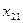 | 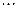 | 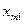 | |
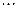 | 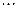 | 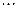 | 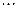 | 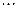 | 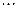 |
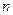 | 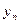 | 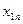 | 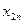 | 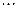 | 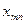 |
На основе данных, содержащихся в этой таблице, вычисляют матрицу коэффициентов парной корреляции 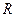 , она симметрична относительно главной диагонали:
, она симметрична относительно главной диагонали:
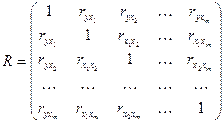
Анализ матрицы коэффициентов парной корреляции используют при построении множественной регрессии.
Одной корреляционной матрицей нельзя полностью описать зависимости между величинами. В связи с этим, в многомерном корреляционном анализе рассматривается две задачи:
· определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ;
· определение тесноты связи между величинами при фиксировании или исключении влияния остальных k величин, при k <(m -2).
Эти задачи решаются с помощью коэффициентов множественной и частной корреляции, соответственно.
Множественный коэффициент корреляции. Решение первой задачи (определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ) осуществляется с помощью выборочного коэффициента множественной корреляции (индекса корреляции) по формуле
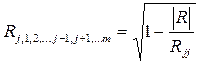 ,
,
где 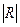 - определитель корреляционной матрицы R;
- определитель корреляционной матрицы R; 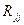 - алгебраическое дополнение элемента rjj той же матрицы R.
- алгебраическое дополнение элемента rjj той же матрицы R.
Квадрат коэффициента множественной корреляции 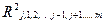 принято называть выборочным множественным коэффициентом детерминации, который показывает, какую долю вариации (случайного разброса) исследуемой величины Хj объясняет вариация остальных случайных величин X1 , X2,..., Xm при их совместном действии.
принято называть выборочным множественным коэффициентом детерминации, который показывает, какую долю вариации (случайного разброса) исследуемой величины Хj объясняет вариация остальных случайных величин X1 , X2,..., Xm при их совместном действии.
Коэффициенты множественной корреляции и детерминации являются величинами положительными, принимающими значения в интервале от 0 до 1. При приближении коэффициента R2 к единице можно сделать вывод о тесноте взаимосвязи случайных величин, но не о ее направлении. Коэффициент множественной корреляции может только увеличиваться, если в модель включать дополнительные переменные и не увеличится, если из имеющихся признаков производить исключение.
Проверка значимости коэффициента множественной корреляции осуществляется путем сравнения расчетного значения критерия Фишера:
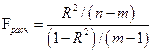
с табличным F табл. Табличное значение критерия определяется заданным уровнем значимости 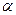 и степенями свободы
и степенями свободы 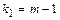 и
и 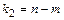 (
(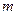 – количество параметров модели). Коэффициент R2 значимо отличается от нуля, если выполняется неравенство
– количество параметров модели). Коэффициент R2 значимо отличается от нуля, если выполняется неравенство
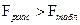 .
.
Частный коэффициент корреляции
Если рассматриваемые случайные величины коррелируют друг с другом, то на величине коэффициента парной корреляции частично сказывается влияние других величин. В связи с этим возникает необходимость исследования частной корреляции между величинами при исключении влияния одной или нескольких других случайных величин.
Выборочный частный коэффициент корреляции определяется по формуле:
‘ 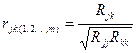 ,
,
где 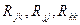 – алгебраические дополнения к соответствующим элементам матрицы
– алгебраические дополнения к соответствующим элементам матрицы 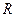 . Частный коэффициент корреляции, так же как и парный коэффициент корреляции изменяется от –1 до +1.
. Частный коэффициент корреляции, так же как и парный коэффициент корреляции изменяется от –1 до +1.
Выражение выборочного частного коэффициента корреляции при условии 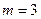 имеет вид
имеет вид

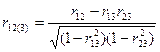 .
.
Коэффициент 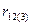 называется коэффициентом корреляции между
называется коэффициентом корреляции между 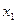 и
и 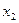 при фиксированном
при фиксированном 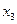 . Он симметричен первичных индексов 1, 2. Его вторичный индекс 3 относится к фиксированной переменной.
. Он симметричен первичных индексов 1, 2. Его вторичный индекс 3 относится к фиксированной переменной.
Проверка значимости частного коэффициента корреляции осуществляется также, как парного коэффициента корреляции, только 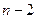 при этом заменяется на
при этом заменяется на 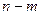 , т.е.вычисляемся статистика Стьюдента
, т.е.вычисляемся статистика Стьюдента
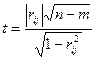 ,
,
где 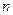 - количество пар наблюдений;
- количество пар наблюдений; 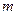 - количество факторов.
- количество факторов.
Коэффициент частной корреляции считается значимым, если 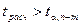 причем значение
причем значение 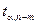 определяется по таблицам распределения Стьюдента:
определяется по таблицам распределения Стьюдента: 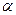 - уровень значимости,
- уровень значимости, 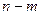 - число степеней свободы.
- число степеней свободы.
Величина 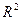 , называемая множественным коэффициентом детерминации, показывает, какую долю вариации исследуемой переменной объясняет вариация остальных переменных.
, называемая множественным коэффициентом детерминации, показывает, какую долю вариации исследуемой переменной объясняет вариация остальных переменных.
Пример
Вычисление коэффициентов парной, множественной и частной корреляции. В табл. 13 представлена информация об объёмах продаж и затратах на рекламу одной фирмы, а также индекс потребительских расходов за ряд текущих лет. Требуется: Построить диаграмму рассеяния (корреляционное поле) для переменных «объёмы продаж» и «индекс потребительских расходов».Определить степень влияния индекса потребительских расходов на объёмы продаж (вычислить коэффициент парной корреляции). Оценить значимость вычисленного коэффициента парной корреляции. Построить матрицу коэффициентов парной корреляции по трем переменным. Найти оценку множественного коэффициента корреляции. Найти оценки коэффициентов частной корреляции.
Таблица 13
Объемы продаж и затраты на рекламу
Объем продаж, тыс. руб.-  | ||||||||||||||||
Затраты на рекламу - 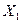 | 4,8 | 3,8 | 8,7 | 8,2 | 9,7 | 14,7 | 18,7 | 19,8 | 10,6 | 8,6 | 6,5 | 12,6 | 6,5 | 5,8 | 5,7 | |
Индекс потребительских расходов, % - 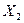 | 98,4 | 101,2 | 103,5 | 104,1 | 107,4 | 108,5 | 108,3 | 109,2 | 110,1 | 110,7 | 110,3 | 111,8 | 112,3 | 112,9 |
Решение.
1) Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение о том, что существует некоторая объективная тенденция прямой линейной связи между значениями переменных x- индекс потребительских расходов и y- объёмы продаж.
В нашем примере диаграмма рассеяния имеет вид, приведенный на рис 3.
2) Промежуточные расчеты при вычислении коэффициента корреляции между переменными x- индекс потребительских расходов и y- объёмы продаж приведены в таблице 3.2..
Средние значения случайных величин Х и Y, которые являются наиболее простыми показателями, характеризующими последовательности 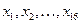 и
и 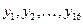 , рассчитаем по формулам, соответственно:
, рассчитаем по формулам, соответственно:

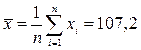
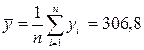 .
.
Дисперсия характеризуют степень разброса значений 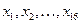 (
(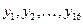 ) вокруг своего среднего
) вокруг своего среднего 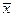 (
(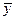 , соответственно)
, соответственно)
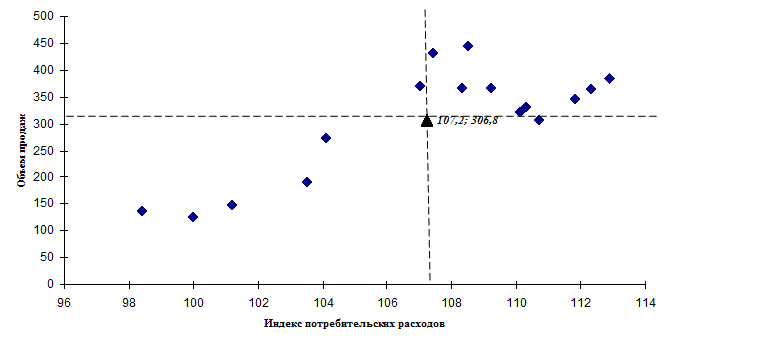
Рис. 3. Диаграмма рассеяния (корреляционное поле).
Стандартные ошибки случайных величин Х и Y рассчитаем по формулам, соответственно:
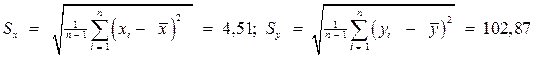
Коэффициент парной корреляции рассчитаем по:
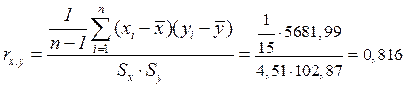
Таблица 14.
Расчетная таблица коэффициента коореляции
| № | Y | X |  |  | 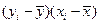 | 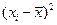 | 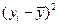 |
| -180,813 | -7,231 | 1307,500 | 52,291 | 32693,160 | |||
| 98,4 | -169,813 | -8,831 | 1499,657 | 77,991 | 28836,285 | ||
| 101,2 | -158,813 | -6,031 | 957,838 | 36,376 | 25221,410 | ||
| 103,5 | -115,813 | -3,731 | 432,125 | 13,922 | 13412,535 | ||
| 104,1 | -32,813 | -3,131 | 102,744 | 9,805 | 1076,660 | ||
| 63,188 | -0,231 | -14,612 | 0,053 | 3992,660 | |||
| 107,4 | 125,188 | 0,169 | 21,125 | 0,028 | 15671,910 | ||
| 108,5 | 138,188 | 1,269 | 175,325 | 1,610 | 19095,785 | ||
| 108,3 | 60,188 | 1,069 | 64,325 | 1,142 | 3622,535 | ||
| 109,2 | 60,188 | 1,969 | 118,494 | 3,876 | 3622,535 | ||
| 110,1 | 14,188 | 2,869 | 40,700 | 8,230 | 201,285 | ||
| 110,7 | 0,188 | 3,469 | 0,650 | 12,032 | 0,035 | ||
| 110,3 | 24,188 | 3,069 | 74,225 | 9,417 | 585,035 | ||
| 111,8 | 38,188 | 4,569 | 174,469 | 20,873 | 1458,285 | ||
| 112,3 | 57,188 | 5,069 | 289,869 | 25,692 | 3270,410 | ||
| 112,9 | 77,188 | 5,669 | 437,557 | 32,135 | 5957,910 | ||
| сумма | 1715,7 | 0,000 | 0,000 | 5681,994 | 305,474 | 158718,438 | |
| среднее | 306,8125 | 107,23125 |
3) Оценим значимость коэффициента корреляции. Для этого рассчитаем значение t – статистики по формуле 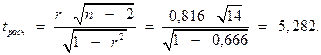 Табличное значение критерия Стьюдента равно: tтабл (α = 0,1; k = n – 2 = 14) =1,76 (см. Приложение 2). Сравнивая числовые значения критериев, видно, что tрасч > tтабл, т.е. полученное значение коэффициента корреляции значимо.
Табличное значение критерия Стьюдента равно: tтабл (α = 0,1; k = n – 2 = 14) =1,76 (см. Приложение 2). Сравнивая числовые значения критериев, видно, что tрасч > tтабл, т.е. полученное значение коэффициента корреляции значимо.
Таким образом, индекс потребительских расходов оказывает весьма высокое влияние на объёмы продаж.
4) Матрица R коэффициентов парной корреляции, для трех факторов будет иметь вид (табл.15):
Таблица 15
Коэффициенты парной корреляции
| Объем реализации | Затраты на рекламу | Индекс потребительских расходов | ||
| Объем реализации | 0,646 | 0,816 | ||
| Затраты на рекламу | 0,646 | 0,273 | ||
| Индекс потребительских расходов | 0,816 | 0,273 |
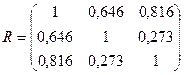 .
.
5) Вычисление множественного коэффициента корреляции.
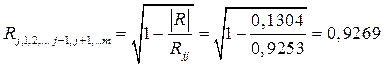 ,
,
где 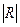 - определитель корреляционной матрицы R равен 0,1304;
- определитель корреляционной матрицы R равен 0,1304; 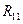 - алгебраическое дополнение 1-го диагонального элемента
- алгебраическое дополнение 1-го диагонального элемента 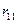 той же матрицы R
той же матрицы R
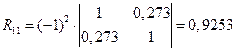 .
.
6) Вычисление коэффициентов частной корреляции.
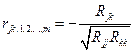
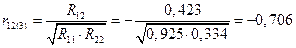 ,
,
где 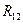 алгебраическое дополнение элемента
алгебраическое дополнение элемента 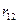 матрицы R, а
матрицы R, а 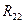 алгебраическое дополнение 2-го диагонального элемента
алгебраическое дополнение 2-го диагонального элемента 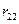 :
:
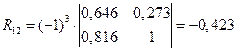
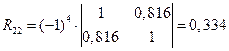 .
.
Коэффициенты частной корреляции можно вычислить, используя коэффициенты парной корреляции:
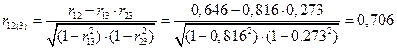
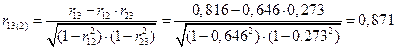 .
.
При отклонении парной статистической зависимости от линейной коэффициент корреляции теряет свой смысл как характеристика тесноты связи. В этом случае можно воспользоваться таким измерителем связи, как индекс корреляции (корреляционное отношение). Корреляционное отношение применяется в случае нелинейной зависимости между признаками и определяется через отношение межгрупповой дисперсии к общей дисперсии.
Применение корреляционного отношения возможно, если характер выборочных данных (количество, плотность расположения на диаграмме рассеяния) допускает, во-первых, их группирование по оси объясняющей переменной и, во-вторых, возможность подсчета «частных» математических ожиданий внутри каждого интервала группирования.
Для определения эмпирического корреляционного отношения совокупность значений результативного признака  разбивают на отдельные группы. В основу группировки кладется исследуемый фактор
разбивают на отдельные группы. В основу группировки кладется исследуемый фактор 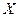 .
.
Когда изучаемая совокупность (в виде корреляционной таблицы) разбивается на группы по одному (факторному) признаку 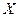 , то для каждой из этих групп можно вычислить соответствующие групповые средние результативного признака. Изменение групповых средних от группы к группе свидетельствует о наличии связи результативного признака с факторным признаком, а примерное равенство групповых средних — об отсутствии связи. Следовательно, чем большую роль в общем изменении результативного признака играет изменение групповых средних (за счет влияния факторного признака), тем сильнее влияние этого признака.
, то для каждой из этих групп можно вычислить соответствующие групповые средние результативного признака. Изменение групповых средних от группы к группе свидетельствует о наличии связи результативного признака с факторным признаком, а примерное равенство групповых средних — об отсутствии связи. Следовательно, чем большую роль в общем изменении результативного признака играет изменение групповых средних (за счет влияния факторного признака), тем сильнее влияние этого признака.
Приведем методику вычисления корреляционного отношения.
Пусть группирование данных произведено, при этом 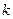 – число интервалов группирования по оси
– число интервалов группирования по оси 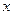 ;
; 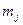
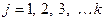 - – количество элементов выборки в
- – количество элементов выборки в 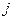 -м интервале группирования;
-м интервале группирования; 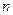 – объем совокупности (
– объем совокупности (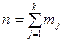 );
); 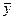 -общее среднее.
-общее среднее.
1. Вычислим среднее значение  в
в 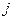 -й группе:
-й группе:
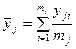 .
.
2.Вычислим общую среднюю  , используя средние значения в каждой группе:
, используя средние значения в каждой группе:
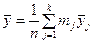 .
.
3. Найдем межгрупповую дисперсию и общую дисперсию:
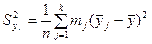 ;
; 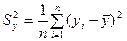 .
.
Корреляционное отношение 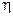 зависимой переменной
зависимой переменной  по независимой переменной
по независимой переменной 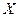 может быть получено из отношения межгрупповой дисперсии к общей дисперсии:
может быть получено из отношения межгрупповой дисперсии к общей дисперсии:
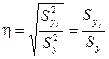 .
.
Величина корреляционного отношения изменяется от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице – о тесной связи.
Корреляционное отношение показывает, сколько процентов вариации признака объясняется вариацией фактора и используется для оценки плотности связи по данным аналитической группировки.
Как показатель тесноты связи корреляционное отношение имеет более универсальный характер, чем линейный коэффициент корреляции, поскольку его использование не ограничивается случаями линейной связи, а факторный признак может быть не количественным, а ранговым и даже номинальным.
 2015-05-13
2015-05-13 3873
3873

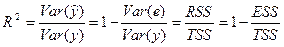 —
—