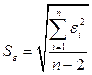Для модели парной регрессии

.

Анализ статистической значимости параметров модели парной регрессии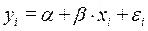

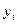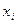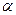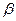Значения , соответствующие данным при теоретических значениях и являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов 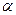и .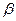

Надежность получаемых оценок 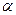и 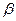зависит от дисперсии случайных отклонений (ошибок). По данным выборки эти отклонения и, соответственно, их дисперсия не оцениваются – в расчетах используются отклонения зависимой переменной 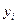от ее расчетных значений 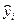: 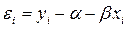. Так как ошибки (остатки) 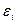нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения этой вариации. Среднеквадратические отклонения коэффициентов известны как стандартные ошибки (отклонения):

,

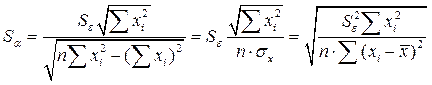
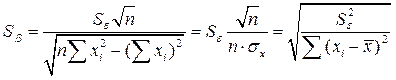где 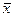- среднее значение независимой переменной х; 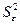стандартная ошибка, вычисляемая по формуле ; .

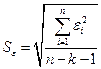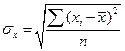Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t–статистики) для соответствующих коэффициентов регрессии:

; .

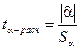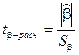Затем расчетные значения 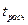сравниваются с табличными t_табл. Табличное значение критерия определяется при (n- 2) степенях свободы (n - число наблюдений) и соответствующем уровне значимости a (0,1; 0,05)

Если расчетное значение t-критерия с 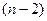степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).

Интервальная оценка параметров модели

Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра :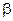

,

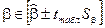свободного члена :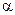

,

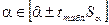где t _табл определяется по таблице распределения Стьюдента для уровня значимости a и числа степеней свободы k = n - 2; 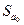, 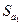– стандартные отклонения, соответственно, свободного члена и коэффициента модели; n – число наблюдений.

Прогнозирование с применением уравнения регрессии. Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.

Прогнозируемое значение переменной получается при подстановке в уравнение регрессии ожидаемой величины фактора :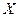

.

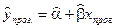Данный прогноз называется точечным. Значение независимой переменной 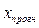не должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.

Вероятность реализации точечного прогноза теоретически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.

доверительные интервалы зависят от следующих параметров:

· от стандартной ошибки;

· удаления 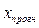от своего среднего значения ;

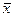· количества наблюдений n;

· уровня значимости прогноза α.

В частности, для прогноза 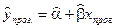будущие значения 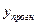с вероятностью (1 - α) попадут в интервал

.

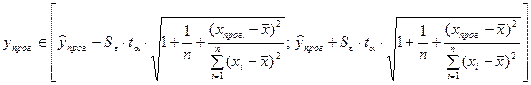Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии хорош только в том случае, если значение фактора 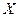не выходит за пределы выборки. Иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.

Пример.

Используя данные предыдущего примера, оценить накопления семьи, имеющей доход 42 тыс. $ и отобразить на графике исходные данные, результаты моделирования и прогнозирования.

Решение.

В предыдущем примере была построена модель зависимости накопления от дохода:

.

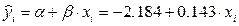Для того, чтобы определить накопления семьи при доходе 42 тыс.$ необходимо подставить значение х_прогн в полученную модель.

y_{прогноз} = - 2.184+0.143*42= 3.827

Величину отклонения от линии регрессии вычисляют по формуле 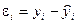, используя данные таблицы 20. Величину 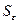находят по формуле

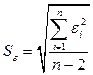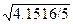= = 0.9112

Таблица 21

Таблица остатков

Наблюдение	Накопления	Предсказанное Y	Остатки	e2
	Y		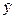e
		3.541	-0.5406	0.2923
		5.688	0.3125	0.0977
		4.256	0.7438	0.5532
	3.5	2.109	1.3906	1.9338
	1.5	2.109	-0.6094	0.3713
	4.5	4.972	-0.4719	0.2227
		2.825	-0.8250	0.6806
Сумма	25.5	25.500	0.0000	4.1516

Коэффициент Стьюдента 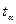для m=5 степеней свободы (m=n-2) и уровня значимости 0.1 равен 2.015. Тогда

U_{(x=42,n=7,a=0.1)} = =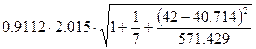

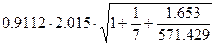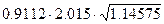= = =1.965

Таким образом, прогнозное значение 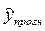=3,827 будет находиться между верхней границей, равной 3.827+1,965=5,792 и нижней границей, равной 3,827-1,965=1,862.

График исходных данных и результаты моделирования приведены на рисунке 5

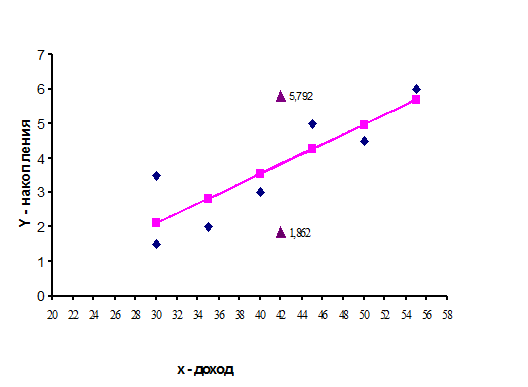
Рис.5. График модели парной регрессии зависимости накопления от дохода.

Линейная модель множественной регрессии имеет вид:

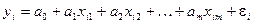
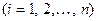
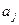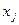коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак , если переменную увеличить на единицу измерения, т. е. 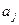является нормативным коэффициентом. Обычно предполагается, что случайная величина 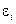имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией .

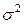Анализ данного уравнения и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения:

,

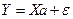где – это вектор зависимой переменной размерности п ´ 1, представляющий собой п наблюдений значений 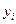; 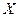- матрица п наблюдений независимых переменных 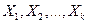, размерность матрицы 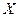равна п ´ (k+1). Дополнительный фактор 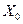, состоящий из единиц, вводится для вычисления свободного члена. В качестве исходных данных могут быть временные ряды или пространственная выборка; 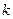- количество факторов, включенных в модель; a — подлежащий оцениванию вектор неизвестных параметров размерности (k+1) ´ 1; параметр 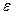— вектор случайных отклонений (возмущений) размерности п ´ 1. 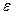отражает тот факт, что изменение 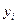будет неточно описываться изменением объясняющих переменных 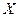, так как существуют и другие факторы, неучтенные в данной модели.

Таким образом,

Y = 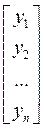, X = , ,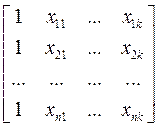

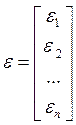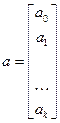
Данное уравнение содержит значения неизвестных пара­метров 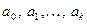. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрес­сии, в которой вместо истинных значений параметров под­ставлены их оценки (а именно такие регрессии и приме­няются на практике), имеет вид

,

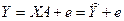где 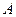– вектор оценок параметров; 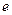– вектор «оценен­ных» отклонений регрессии, остатки регрессии 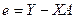; 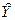– оценка значе­ний , равная .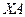

Согласно методу наименьших квадратов, вектор- столбец оценок коэффициентов регрессии вычисляется по формуле

Формулу для вычисления параметров регрессионного уравнения приведем без вывода

,

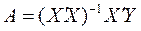где 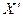– транспонированная матрица; 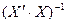– обратная матрица.

Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т. е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы ис­ходных данных линейно независимы. Для экономических показате­лей это условие выполняется не всегда. Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости уравнений, что делает вычисле­ние параметров либо невозможным, либо затрудняет содержатель­ную интерпретацию параметров модели. Мультиколлинеарность может возникать в силу разных причин. На­пример, несколько независимых переменных могут иметь общий вре­менной тренд, относительно которого они совершают малые колебания. В частности, так может случиться, когда значения одной независимой переменной являются лагированными значениями другой. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0.8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени свя­зан с зависимой переменной.

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблю­даемым данным проводится на основе анализа остатков - .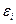

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Для оценки качества модели множественной регрессии вычисляют коэффициент множественной корреляции (индекс корреляции) 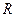и коэффициент детерминации 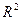. Чем ближе к 1 значение этих характеристик, тем выше качество модели.

В многофакторной регрессии добавление дополнительных объ­ясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скор­ректирован с учетом числа независимых переменных. Скоррек­тированный R², или 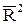_, рассчитывается так:

,

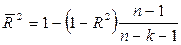где n — число наблюдений; k — число независимых переменных.

Для проверки значимости модели регрессии используется F-критерий Фишера, вычисляемый по формуле:

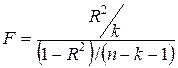
Если расчетное значение с n₁= к и n₂ = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

Анализ статистической значимости параметров модели

значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

,

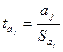где 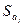– это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии 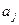.Величина 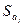представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии 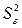и j -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.

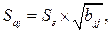
где 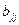- диагональный элемент матрицы .

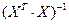Если расчетное значение t-критерия с (n - k - 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели, при этом оставшиеся в модели параметры должны быть пересчитаны.

Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, b - коэффициенты ).

Важную роль при оценке влияния факторов играют коэффициен­ты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени ко­леблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности 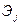и бета-коэффициенты 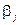, которые рассчитываются соответственно по формулам:

,

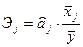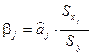
где 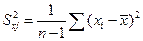– среднеквадратическое отклонение фактора ,

.

.

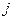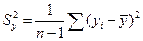Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора 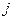на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины средне­го квадратического отклонения S_y изменится зависи­мая переменная Y с изменением соответствующей независимой пере­менной 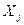на величину своего среднеквадратического отклонения при фиксирован­ном на постоянном уровне значении остальных независимых пере­менных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов мож­но оценить по величине дельта - коэффициентов :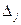

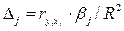
где 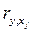— коэффициент парной корреляции между фактором 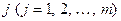и зависимой переменной.

Использование многофактор­ных моделей для анализа и прогнозирования развития экономических систем.

Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Обычно термин «прогнозирование» используется в тех ситуациях, когда требуется предсказать состояние системы в будущем. Для регрессионных моделей он имеет, однако, более широкое значение. Как уже отмечалось, данные могут не иметь временной структуры, но и в этих случаях вполне может возникнуть задача оценки значения зависимой переменной для некоторого набора независимых, объясняющих переменных, которых нет в исходных наблюдениях. Именно в этом смысле — как построение оценки зависимой переменной — и следует понимать прогнозирование в эконометрике.

При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.