Уравнение Менделеева – Клайперона( уравнение идеального газа)

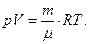
(6.10)

где р – давление; V – объем; Т – термодинамическая температура; М – молярная масса газа; R = 8,31 Дж/(мольּ∙К) – молярная газовая постоянная; m/М = ν – количество вещества.

Уравнение (6.10) представляет собой наиболее общую форму записи уравнения состояния идеального газа. Введем так называемую постоянную Больцмана k, равную от­ношению универсальной газовой постоянной R к числу Аво­гадро N_А:

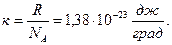
(6.11)

Основное уравнение кинетиче­ской теории газов:

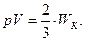
(6.12)

Из него следует, что произведение численных значений давления идеального газа и его объема равно двум третям величины кинетической энергии поступательного движения всех его молекул. Для однородного газа массы всех молекул одинаковы (m₁ = m₀), а скорости 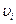различны. Поэтому 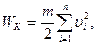и становится целесообразным ввести понятие средней квадратич­ной скорости.

Средней квадратичной скоростью υ_КВ поступательного движения молекул газа называется корень квадратный из среднего арифме­тического квадратов скоростей поступательного движения всех его молекул:

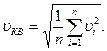
(6.13)

С другой стороны, по уравнению Менделеева — Клапейрона (6.10):

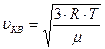
(6.14)

Поскольку m = m₀N_А, где m₀ - масса одной молекулы, a N_А - число Авогадро, то из уравнения (6.14) следует, что

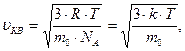
(6.15)

где k - постоянная Больцмана.

Средняя кинетическая энергия по­ступательного движения молекулы идеального газа:

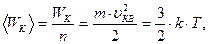
(6.16)

где k – постоянная Больцмана.

Таким образом, абсолют­ная температура является мерой средней кинетической энергии поступательного дви­жения молекул идеального газа. Однако в области температур, близких к абсолют­ному нулю, этот результат оказывается неверным.

Рис. 6.4. Графическое изображение зависимости средней кинетической энергии поступательного движения молекулы идеального газа от температуры

Закон распределения молекул по скоростям имеет следующий вид:

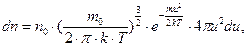
(6.17)

где m - масса молекулы; k - постоянная Больцмана; Т - аб­солютная температура; n₀ – число молекул газа в единице объема; u – скорость.

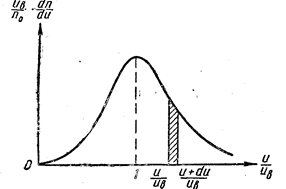
Рис. 6.5. Кривая закона распределения молекул по скоростям

Закон максвелловского распределения молекул по скоростям может быть записан также в виде:

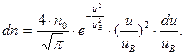
(6.18)

Закон распределения скоростей позволяет подсчитать ве­личину средней арифметической скорости и поступательного движения молекул идеального газа. Расчет приводит к следую­щей формуле:

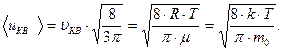
(6.19)

Таким образом, существуют три скорости, характеризующие состояние газа:

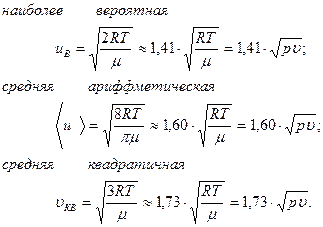
(6.20)

Закон Дальтона для давления смеси n идеальных газов

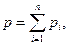
(6.21)

где p_i – парциальное давление i -го компонента смеси.