Тема 3.2. Логарифмы и их свойства. Преобразование и вычисление логарифмических выражений (4часа)
Понятие логарифма.
Задача 1. Найти положительный корень уравнения 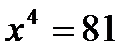 .
.
По определению арифметического корня имеем 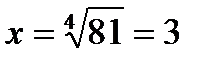 .
.
Задача 2. Решить уравнение 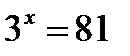 .
.
Запишем данное уравнение так: 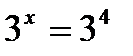 , откуда
, откуда 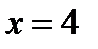 .
.
В задаче 1 неизвестным является основание степени, а в задаче 2 – показатель степени.
Способ решения второй задачи состоял в том, что левую и правую части уравнений удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 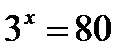 таким способом решить не удается. Однако это уравнение имеет корень. Чтобы решать такие уравнения, вводится новое понятие - логарифм. Чуть забегая вперед, скажем, что корень уравнения
таким способом решить не удается. Однако это уравнение имеет корень. Чтобы решать такие уравнения, вводится новое понятие - логарифм. Чуть забегая вперед, скажем, что корень уравнения 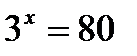 обозначается символом
обозначается символом 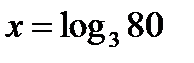 .
.
Остановимся теперь на понятии логарифма числа. Очень часто приходится решать задачу: известно, что 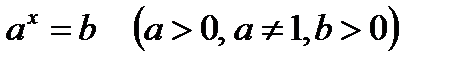 ; необходимо найти показатель степени х, т.е. решать задачу, обратную возведению в степень. При нахождении этого показателя степени х и возникает понятие логарифма числа b по основанию a. (
; необходимо найти показатель степени х, т.е. решать задачу, обратную возведению в степень. При нахождении этого показателя степени х и возникает понятие логарифма числа b по основанию a. (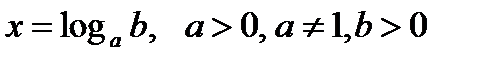 ). Дадим точное определение.
). Дадим точное определение.
Определение. Логарифмом положительного числа b по положительному и отличному от единицы основанию a, называется показатель степени, в которую нужно возвести число a, чтобы получить число b.
Например, 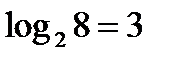 так как
так как 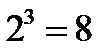 ;
; 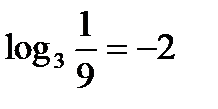 так как
так как 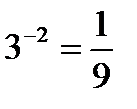 ;
; 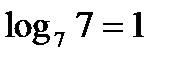 так как
так как 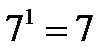 ;
; 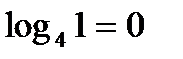 так как
так как 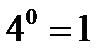 .
.
Определение логарифма можно кратко записать так: 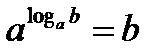 . Это равенство справедливо при
. Это равенство справедливо при 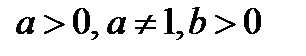 . Его называют основным логарифмическим тождеством.
. Его называют основным логарифмическим тождеством.
Например, 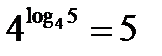 ,
, 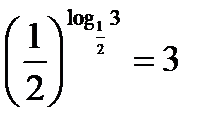 .
.
Операция нахождения логарифма числа называют логарифмированием. Операция логарифмирования и возведение в степень с соответствующим основанием взаимообратны по отношению друг к другу, т.к. 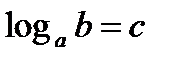 и
и 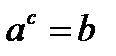 - одна и та же зависимость между числами
- одна и та же зависимость между числами 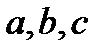 .
.
Задача 2. Вычислить 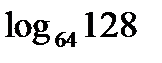 .
.
Решение. Обозначим  . По определению логарифма
. По определению логарифма 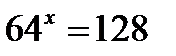 .
. 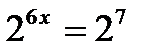 , откуда
, откуда 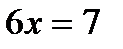 ,
, 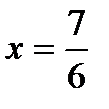
Ответ: 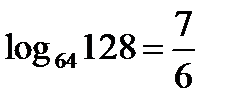 .
.
Задача 3. Вычислить 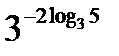 .
.
Решение. Используя свойства степени и основное логарифмическое тождество, находим 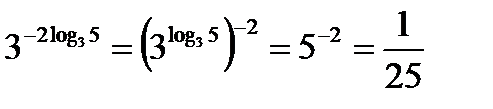 .
.
 2015-05-13
2015-05-13 676
676







