В математике и ее приложениях часто встречается логарифмическая функция 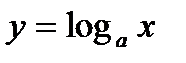 , где
, где 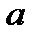 -заданное число,
-заданное число, 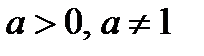 .
.
Свойства логарифмической функции:
10. 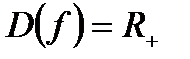 . (Это свойство следует из определения логарифма, так как выражение
. (Это свойство следует из определения логарифма, так как выражение 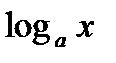 имеет смысл только при
имеет смысл только при 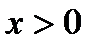 )
)
20. 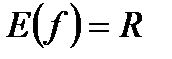 . (это следует из того, что для любого действительного числа b есть такое положительное число х, что
. (это следует из того, что для любого действительного числа b есть такое положительное число х, что 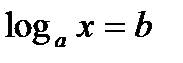 , т.е уравнение
, т.е уравнение 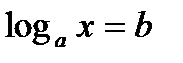 имеет корень. Такой корень существует и равен
имеет корень. Такой корень существует и равен 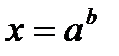 , так как
, так как 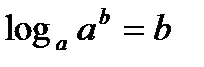 )
)
30. Логарифмическая функция 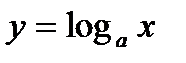 является возрастающей на промежутке
является возрастающей на промежутке 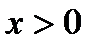 , если
, если 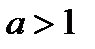 , и убывающей, если
, и убывающей, если 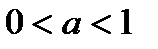 .
.
[[ Пусть 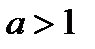 . Докажем, что если
. Докажем, что если 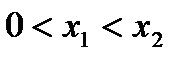 , то
, то 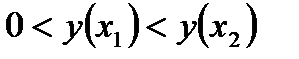 , т. е.
, т. е. 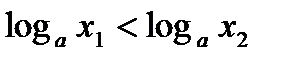 . Пользуясь основным логарифмическим тождеством, условие
. Пользуясь основным логарифмическим тождеством, условие 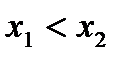 можно записать так:
можно записать так: 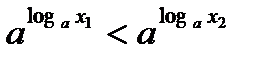 . Из этого неравенства по свойству степени с основанием
. Из этого неравенства по свойству степени с основанием 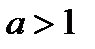 следует, что
следует, что 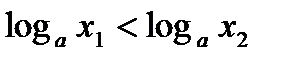 .
.
Пусть 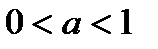 . Докажем, что если
. Докажем, что если 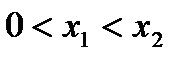 , то
, то 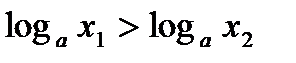 . Записав условие условие
. Записав условие условие 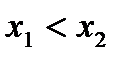 в виде
в виде 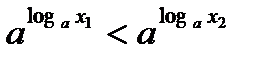 получим
получим 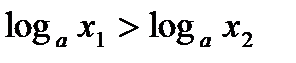 , т.к.
, т.к. 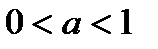 .]]
.]]
Отметим, что справедливы и следующие два утверждения: если 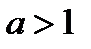 и
и 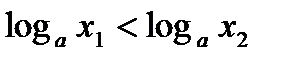 , где
, где 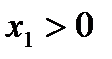 ,
, 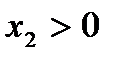 , то
, то 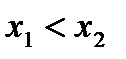 ; если
; если 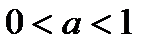 и, то
и, то 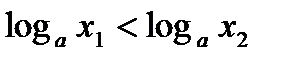 , где
, где 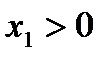 ,
, 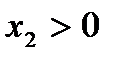 , то
, то 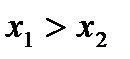
40. Если 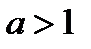 , то функция
, то функция 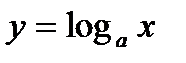 принимает положительные значения при
принимает положительные значения при 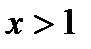 , отрицательные при
, отрицательные при 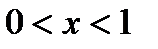 . Если
. Если 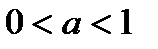 , то функция
, то функция 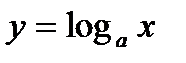 принимает положительные значения при
принимает положительные значения при 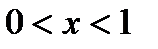 , отрицательные при
, отрицательные при 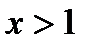 .
.
[[Это следует из того, что функция 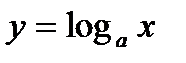 принимает значение, равное нулю, при
принимает значение, равное нулю, при 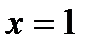 и является возрастающей на промежутке
и является возрастающей на промежутке 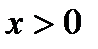 , если
, если 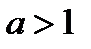 и убывающей, если
и убывающей, если 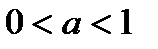 ]].
]].
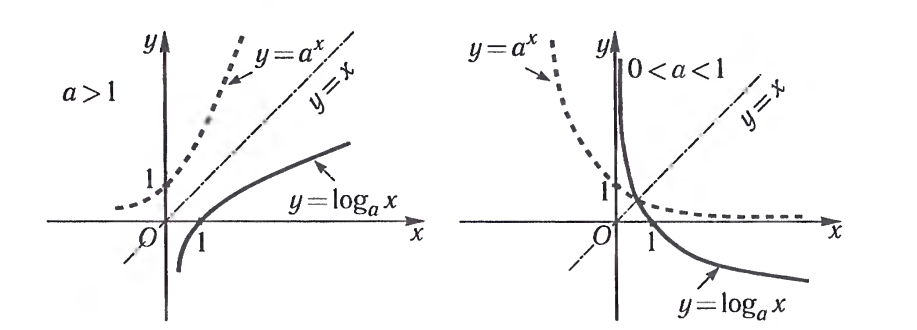
Из рассмотренных свойств логарифмической функции 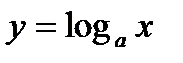 следует, что ее график расположен правее оси Оу и имеет вид, указанный на рисунке.
следует, что ее график расположен правее оси Оу и имеет вид, указанный на рисунке.
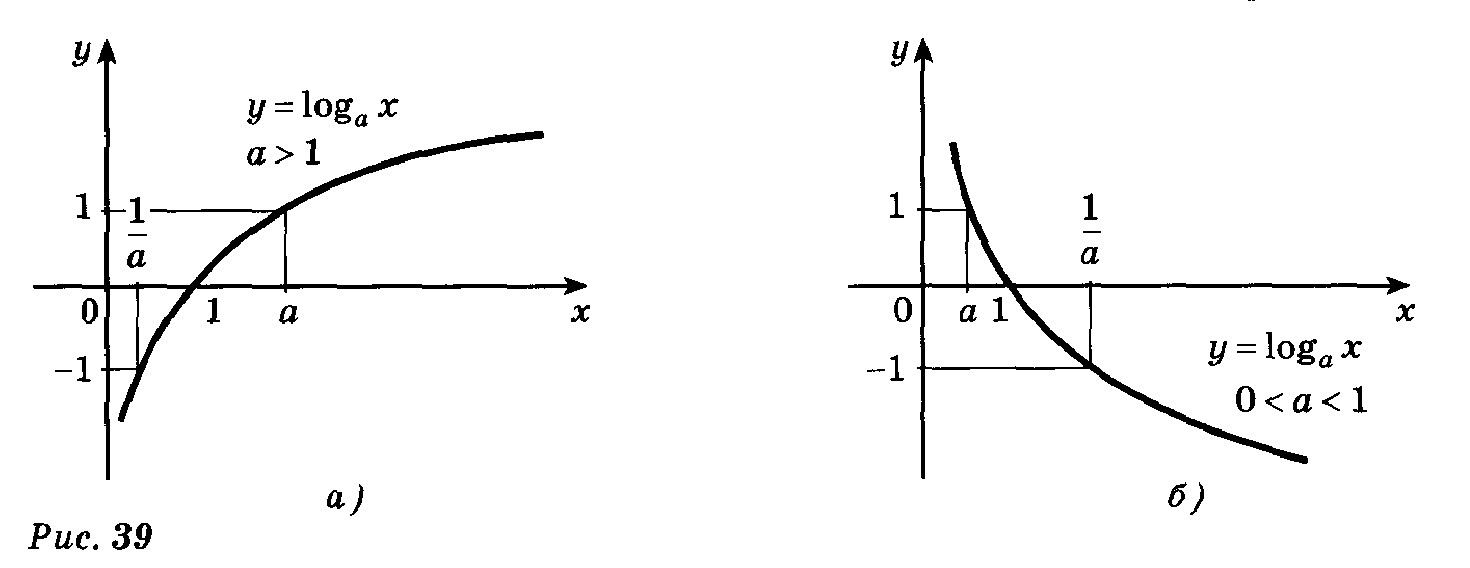
Отметим, что график любой логарифмической функции 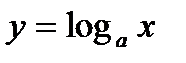 проходит через точку
проходит через точку 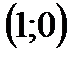 . При решении уравнений часто используется следующая теорема:
. При решении уравнений часто используется следующая теорема:
ТЕОРЕМА. Если 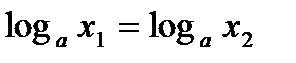 , где
, где 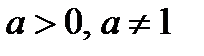 ,
, 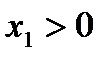 ,
, 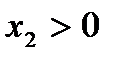 , то
, то 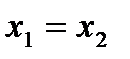 .
.
Задача 1. Решить уравнение 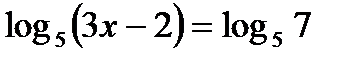 .
.
Решение. Используя доказанную теорем, получаем 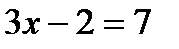 , откуда
, откуда 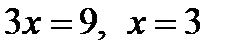 .
.
Ответ: {3}.
Задача 2. Решить неравенство 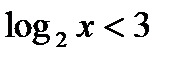 .
.
Решение. Пользуясь тем, что 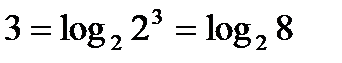 , запишем данное неравенство в виде
, запишем данное неравенство в виде 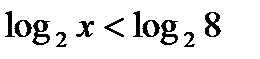 .Так как функция
.Так как функция 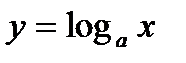 определена при
определена при 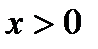 и возрастает, то неравенство
и возрастает, то неравенство 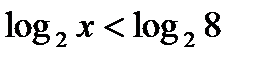 выполняется при
выполняется при 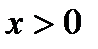 и
и 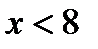 .
.
Ответ: 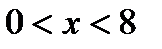 .
.
Логарифмическая функция 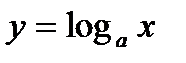 и показательная функция
и показательная функция 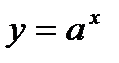 , где
, где 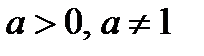 взаимно обратны.
взаимно обратны.
[[Решая уравнение 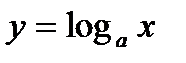 относительно
относительно 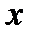 получаем
получаем 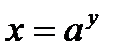 ; меняя местами
; меняя местами 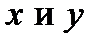 , имеем
, имеем 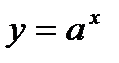 .]]
.]]
Задача 3. Построить график функции 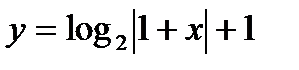 .
.
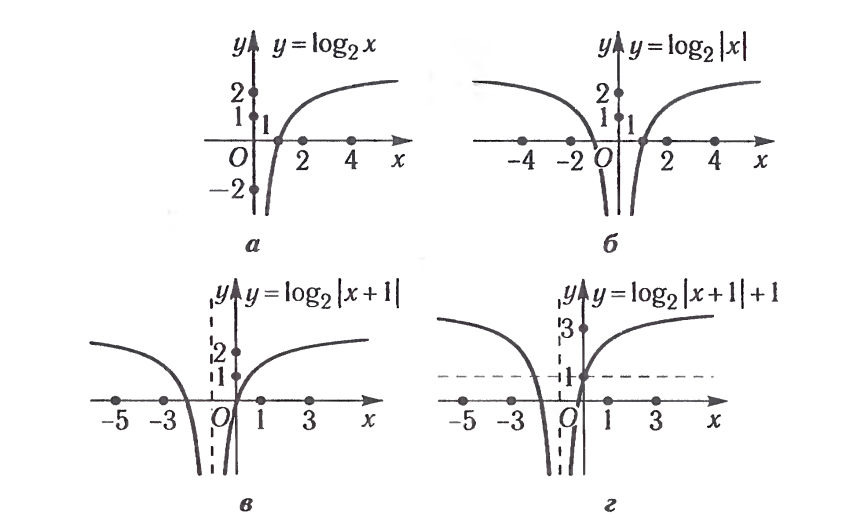
Решение. График данной функции получается из графика функции 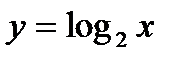 по следующей схеме:
по следующей схеме: 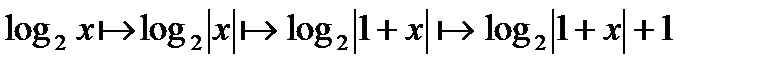 .
.

Задача 4. Является ли функция 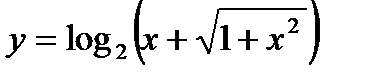 четной или нечетной?
четной или нечетной?
Решение.
ООФ: 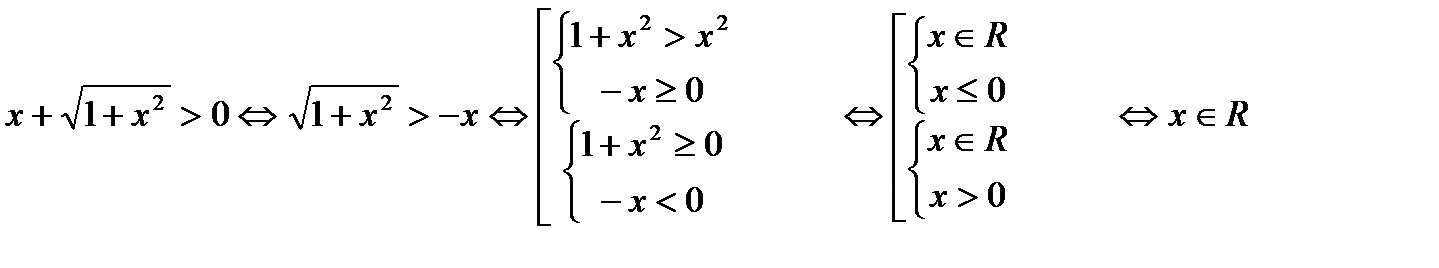
Таким образом, область определения данной функции симметрична относительно начала координат.
Далее, для любого х справедлива следующая цепочка равенств:
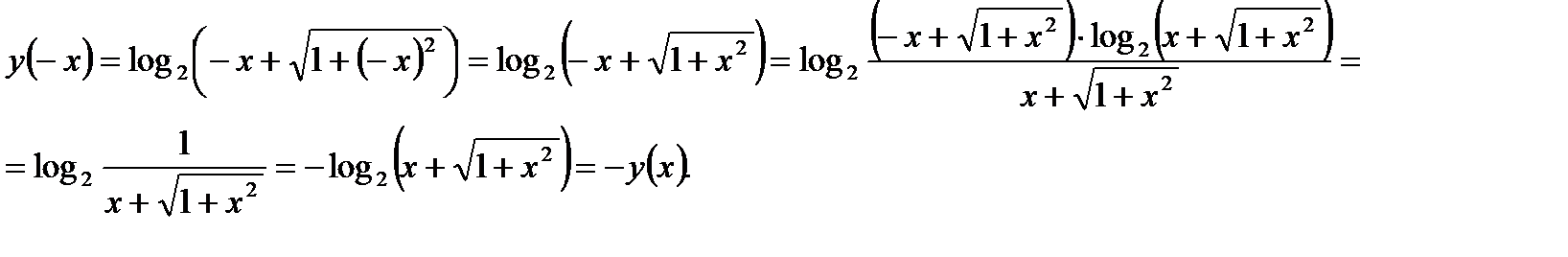
Так как область определения данной функции симметрична относительно начала координат и 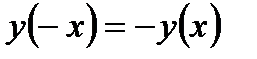 , то функция является нечетной.
, то функция является нечетной.

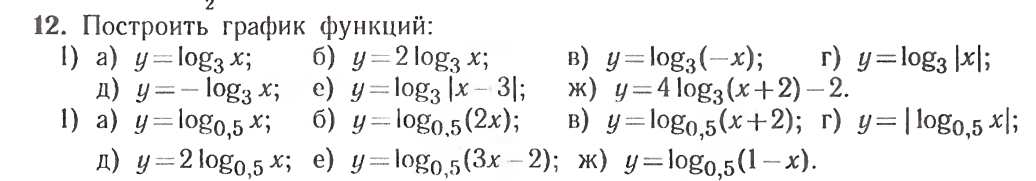
 2015-05-13
2015-05-13 1418
1418