Тема 3.3. Показательная, степенная функции, их свойства и графики. Логарифмическая функция, ее свойства и график. (4 часа)
Степенные функции, их свойства и графики.
Функции вида 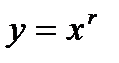 (где
(где 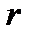 - любое действительное число) называют степенными функциями.
- любое действительное число) называют степенными функциями.
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях 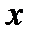 и
и 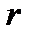 имеет смысл степень
имеет смысл степень 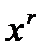 .
.
Рассмотрим различные случаи в зависимости от показателя степени 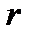 .
.
Ø Показатель 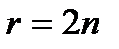 - четное натуральное число. - четное натуральное число. 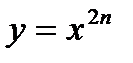 | |
1) 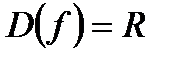 | 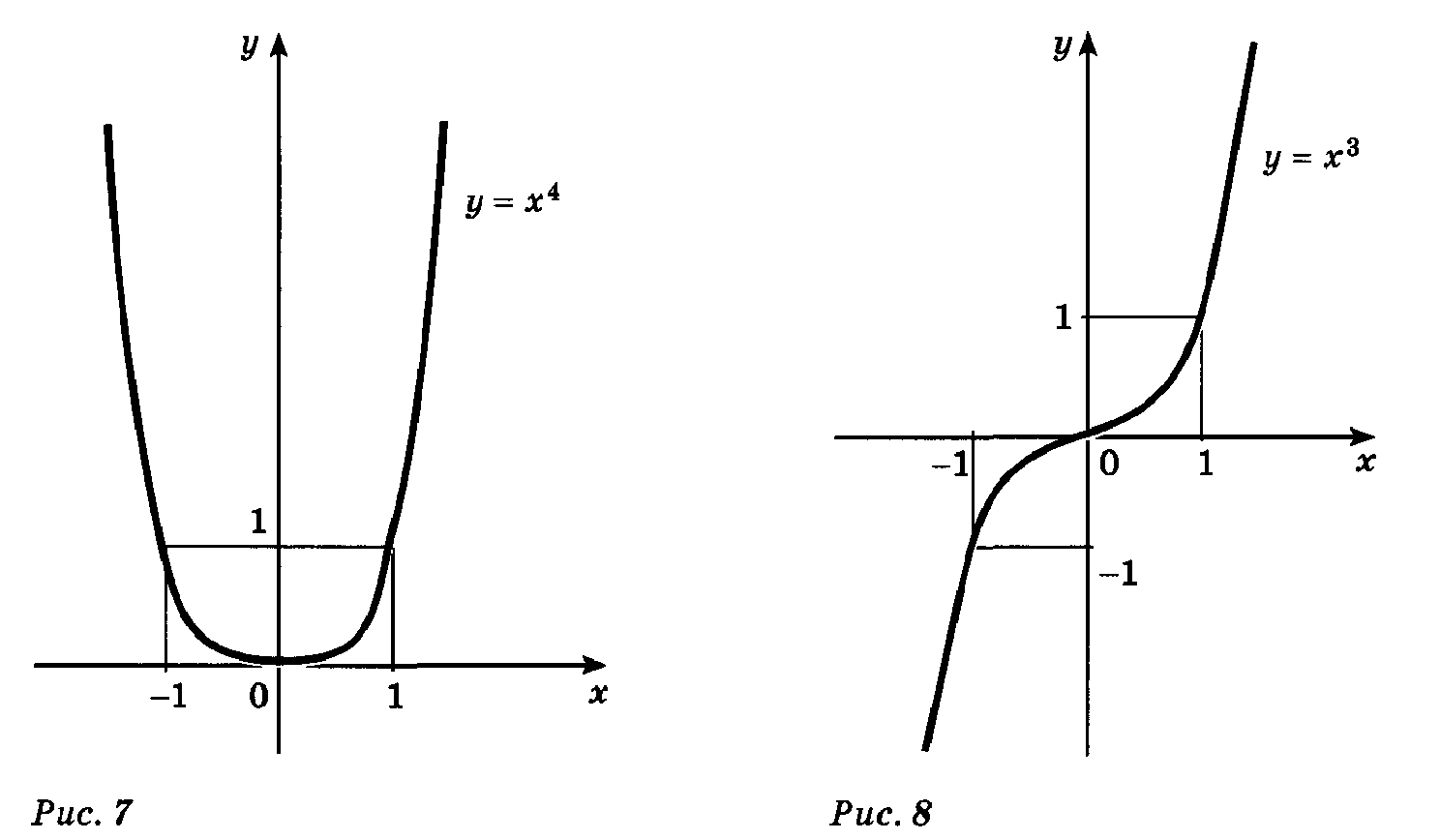 |
2) 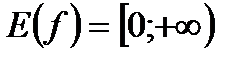 | |
3)функция 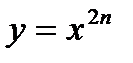 четная, так как четная, так как 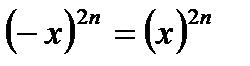 | |
4) убывает на 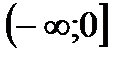 , возрастает на , возрастает на 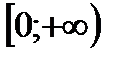 | |
Ø Показатель 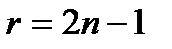 - нечетное натуральное число. - нечетное натуральное число. 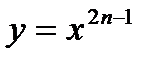 | |
1) 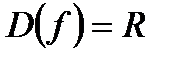 |  |
2) 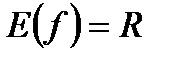 | |
3)функция 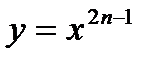 четная, так как четная, так как 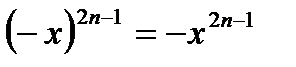 | |
4) возрастает на 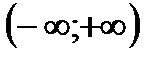 | |
Ø Показатель 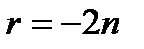 , где , где 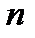 - натуральное число. - натуральное число. 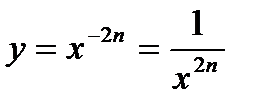 | |
1) 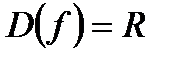 , кроме , кроме 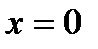 | 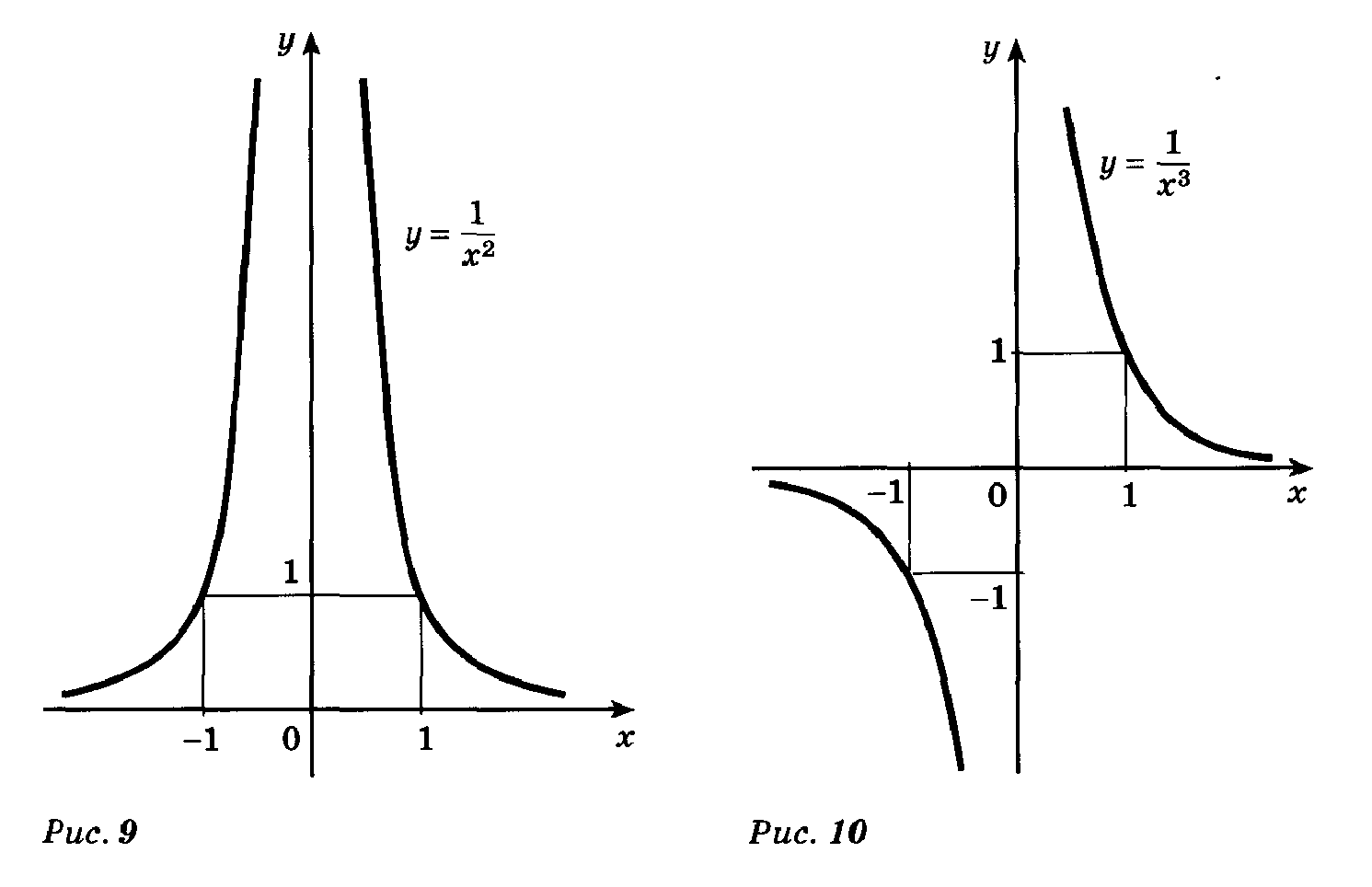 |
2) 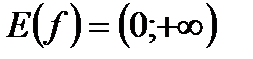 | |
3) функция 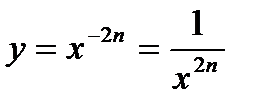 четная, так как четная, так как 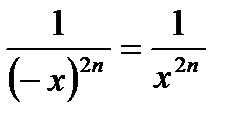 | |
4)) убывает на 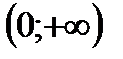 , возрастает на , возрастает на 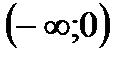 |
Ø Показатель 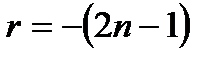 , где , где 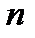 - натуральное число. - натуральное число. 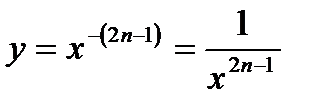 | |
1) 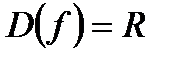 , кроме , кроме 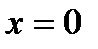 |  |
2) 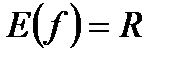 , кроме , кроме 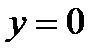 | |
3) функция 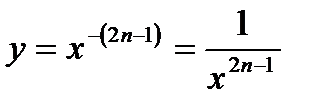 нечетная, так как нечетная, так как 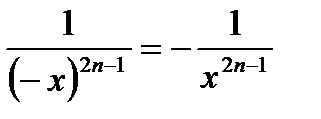 | |
4)) убывает на 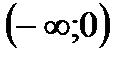 и и 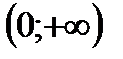 . . |
Ø Показатель 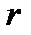 - положительное действительное нецелое число. - положительное действительное нецелое число. 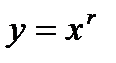 | |
1) 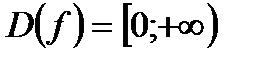 . 2) . 2) 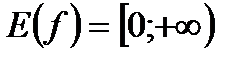 . 3) функция общего вида. 4) возрастает на . 3) функция общего вида. 4) возрастает на 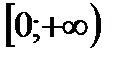 . . | |
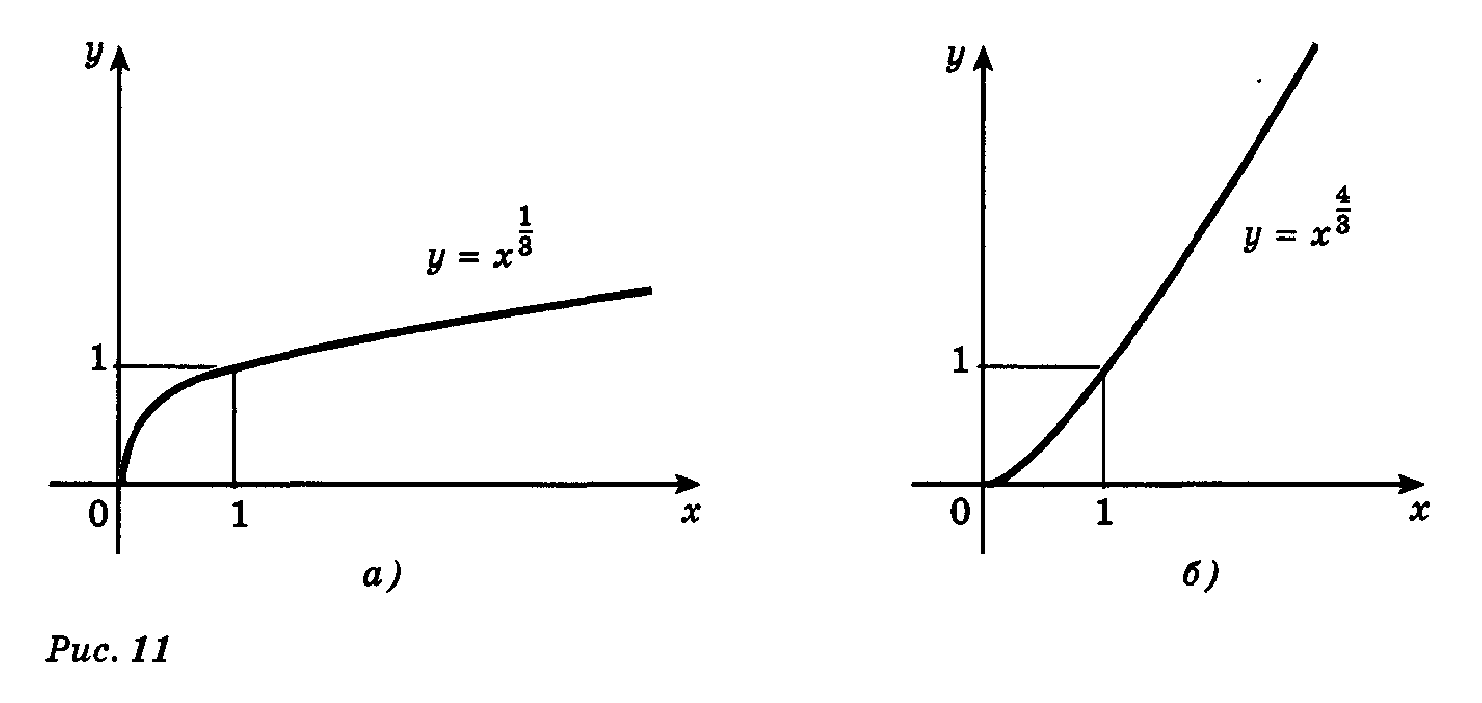 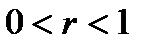 | 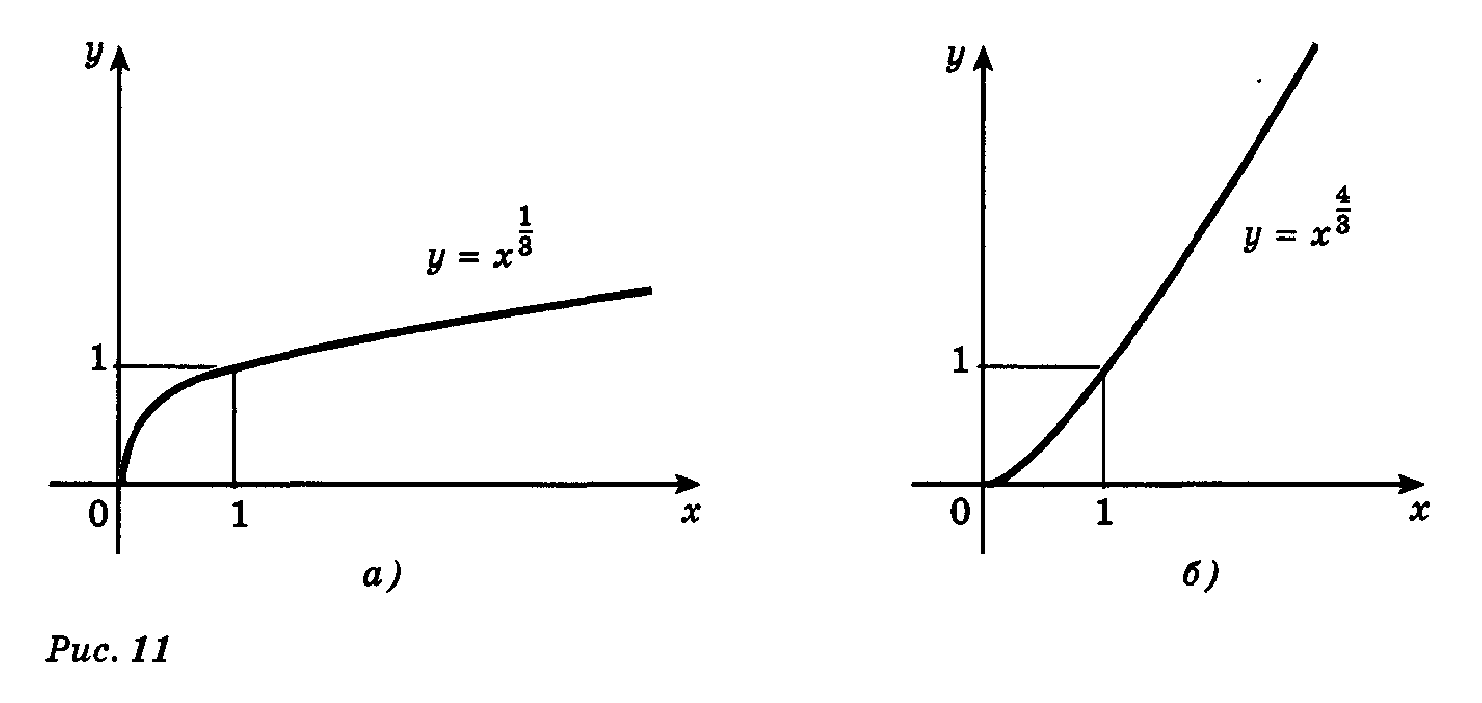 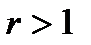 |
Ø Показатель 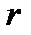 - отрицательное действительное нецелое число. - отрицательное действительное нецелое число. 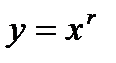 | |
1) 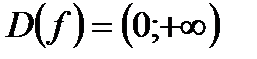 . 2) . 2) 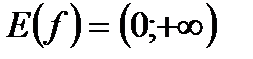 . 3) функция общего вида. 4) убывает на . 3) функция общего вида. 4) убывает на 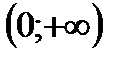 . . | 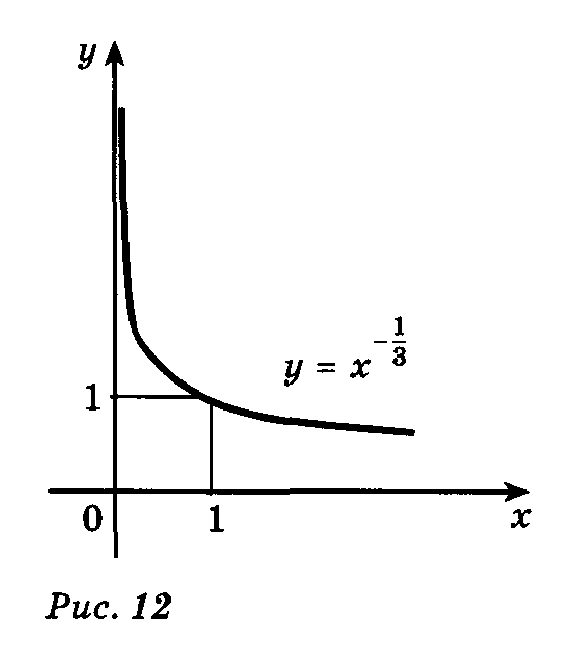 |
 2015-05-13
2015-05-13 1226
1226