Вспомним основные свойства степени. Пусть 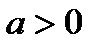 ,
, 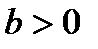 ,
, 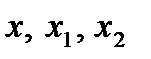 - любые действительные числа. Тогда
- любые действительные числа. Тогда

В практике часто используются функции 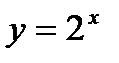 ,
, 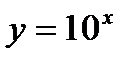 ,
,
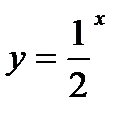 ,
, 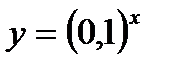 и т.д., т.е. функция вида
и т.д., т.е. функция вида 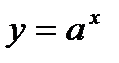 , где
, где 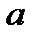 - заданное число,
- заданное число, 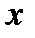 - переменная. Такие функции называются показательными. Это объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени – заданное число.
- переменная. Такие функции называются показательными. Это объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени – заданное число.
Определение. Показательной функцией называется функция 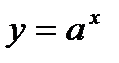 , где
, где 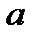 - заданное число,
- заданное число, 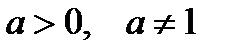 .
.
Свойства показательной функции:
10. 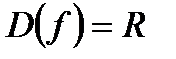 . (Это свойство следует из того, что степень
. (Это свойство следует из того, что степень 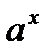 , где
, где 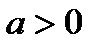 , определена для всех
, определена для всех 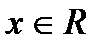 )
)
20. 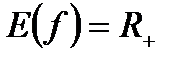 .
.
30. Показательная функция 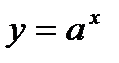 является возрастающей на множестве всех действительных чисел, если
является возрастающей на множестве всех действительных чисел, если 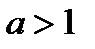 , и убывающей, если
, и убывающей, если 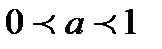 .(следует из свойств 8 и 9).
.(следует из свойств 8 и 9).
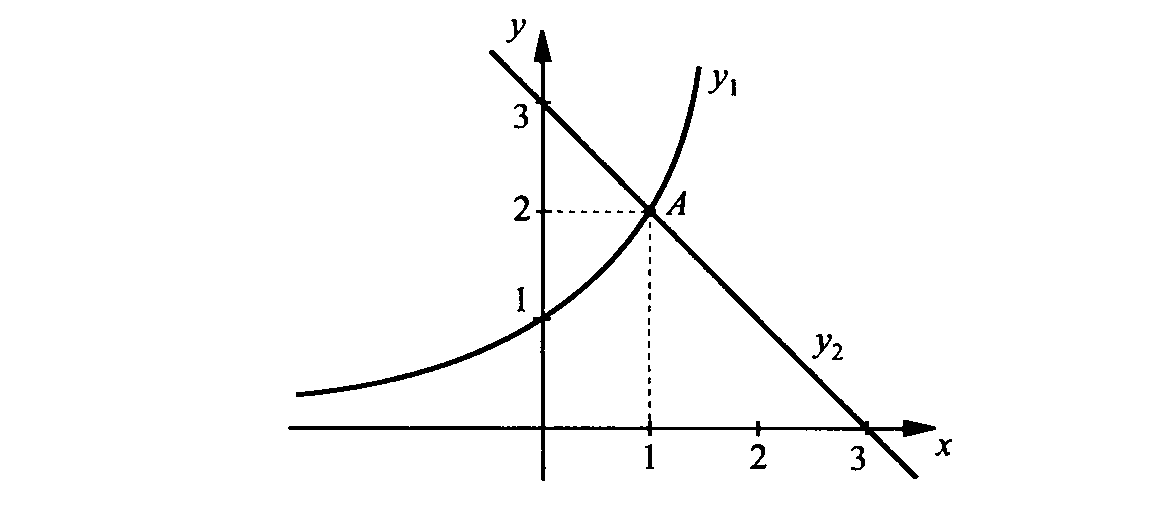
Построим графики функции 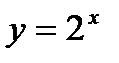 и
и 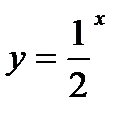 , используя рассмотренные свойства и построив несколько точек, принадлежащих графику.
, используя рассмотренные свойства и построив несколько точек, принадлежащих графику.
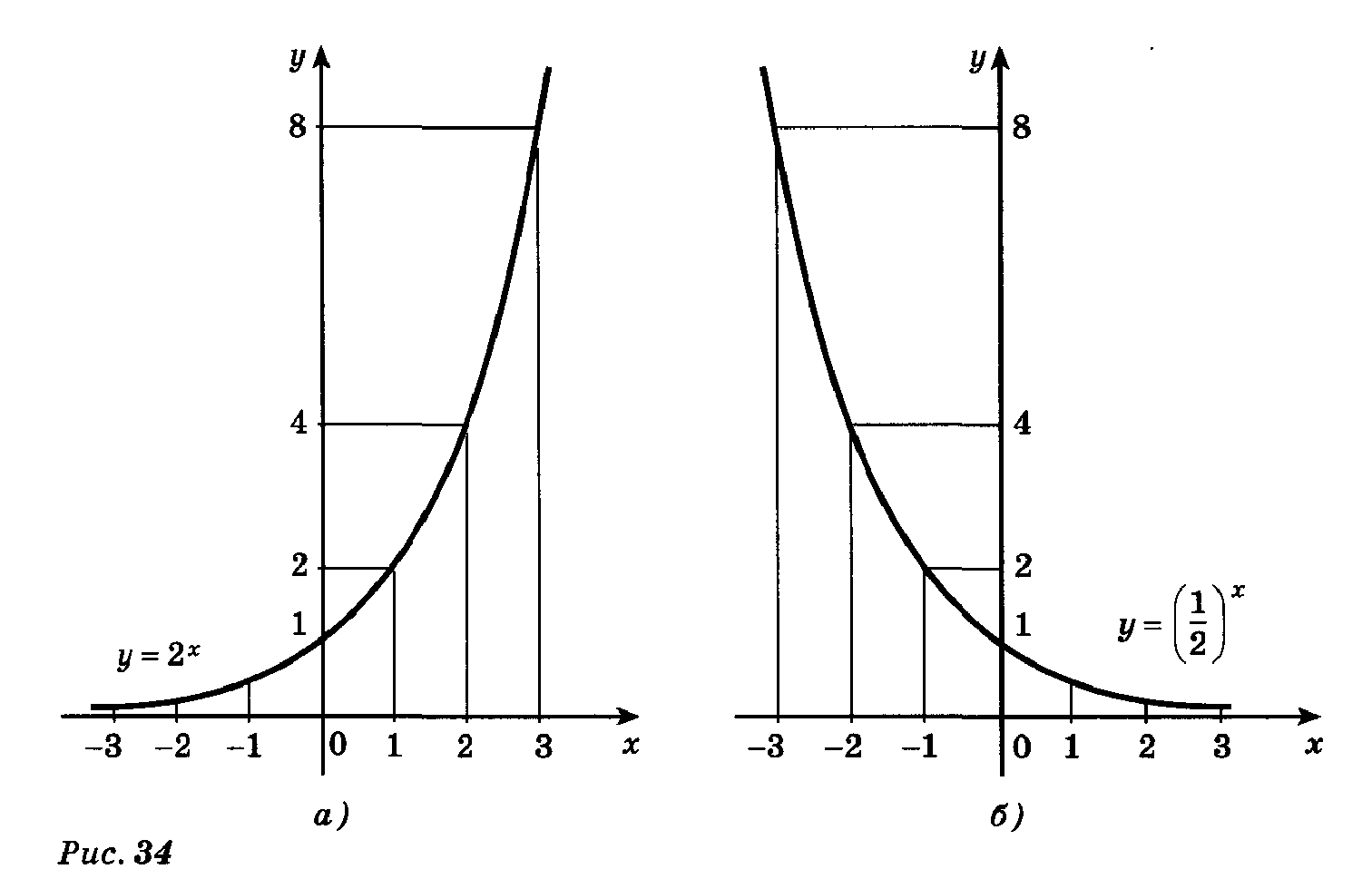
График функции 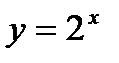 проходит через точку
проходит через точку 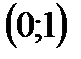 и расположен выше оси Ох. Если
и расположен выше оси Ох. Если 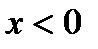 и убывает, то график быстро приближается к оси Ох (но не пересекает его); если
и убывает, то график быстро приближается к оси Ох (но не пересекает его); если 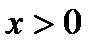 и возрастает, то график быстро поднимается вверх. Такой же вид имеет график любой функции
и возрастает, то график быстро поднимается вверх. Такой же вид имеет график любой функции 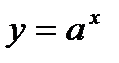 , если
, если 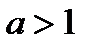 .
.
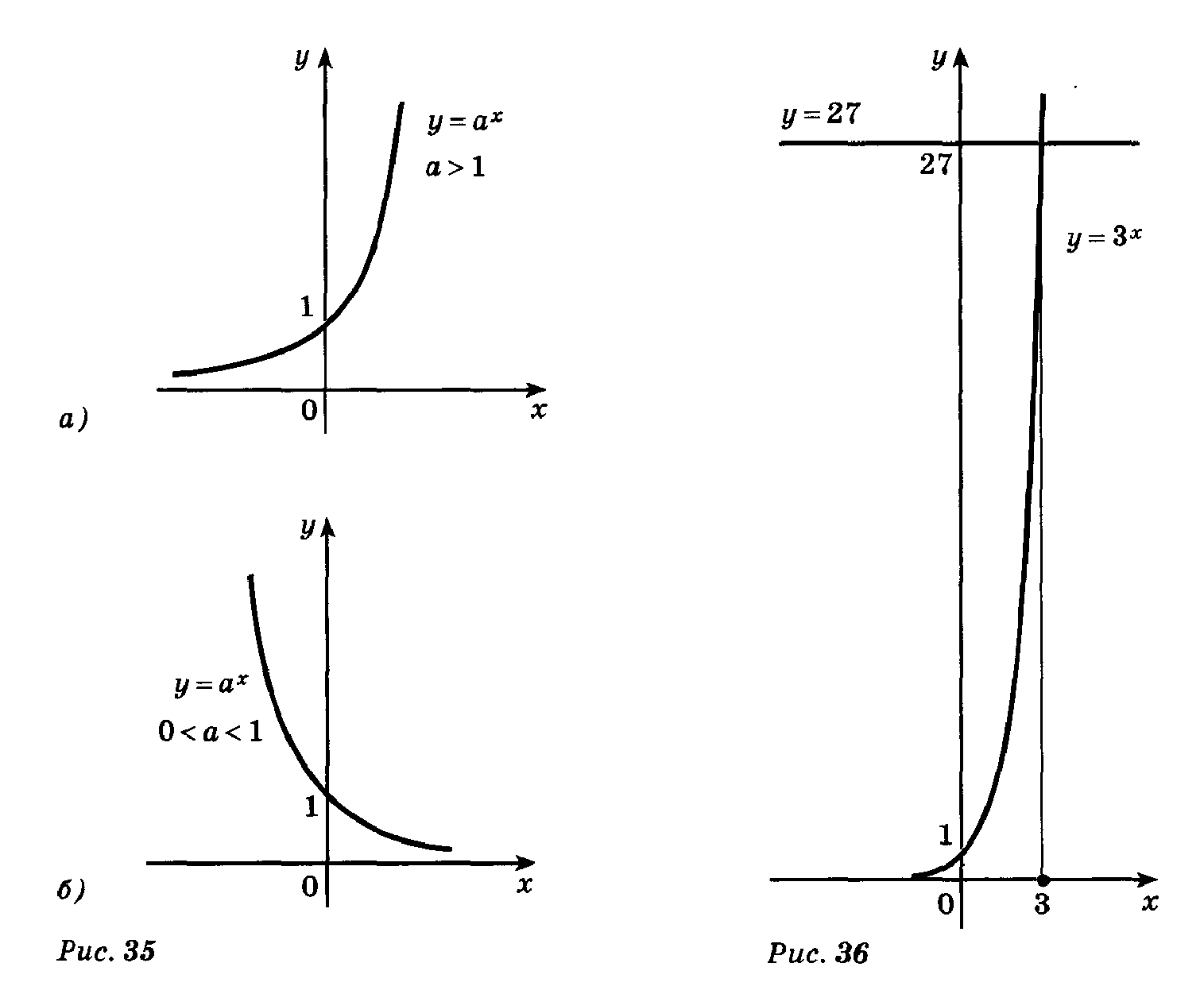
График функции 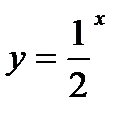 также проходит через точку
также проходит через точку 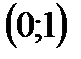 и расположен выше оси Ох. Если
и расположен выше оси Ох. Если 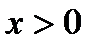 и возрастает, то график быстро приближается к оси Ох (но не пересекает его); если
и возрастает, то график быстро приближается к оси Ох (но не пересекает его); если 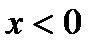 и убывает, то график быстро поднимается вверх. Такой же вид имеет график любой функции
и убывает, то график быстро поднимается вверх. Такой же вид имеет график любой функции 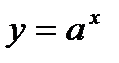 , если
, если 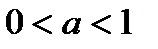 .
.

Показательная функция часто используется при описании различных физических процессов. Так, радиоактивный распад описывается формулой 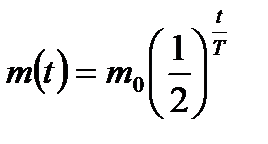 , где \
, где \ 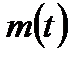 - масса радиоактивного вещества в момент времени
- масса радиоактивного вещества в момент времени 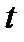 ;
; 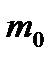 - масса радиоактивного вещества в начальный момент времени
- масса радиоактивного вещества в начальный момент времени 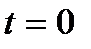 ,
, 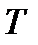 - период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
- период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
С помощью показательной функции выражается давление воздуха в зависимости от высоты подъема, ток самоиндукции в катушке после включения постоянного напряжения и т. д.
Задача 1. Решить уравнение 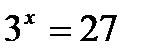 .
.
Решение. По свойству 20 показательной функции данное уравнение имеет корень,
т.к. 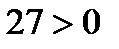 . Одним из корней является число
. Одним из корней является число 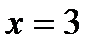 , так как
, так как 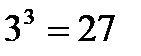 . Других корней нет, так как функция
. Других корней нет, так как функция 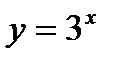 возрастает на всей числовой прямой, и поэтому
возрастает на всей числовой прямой, и поэтому 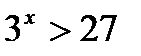 при
при 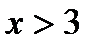 и
и 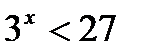 при
при 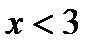 .
.

Ответ: 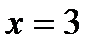 .
.
Задача 2. Сравнить числа 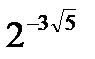 и
и 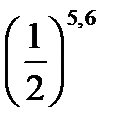 .
.
Решение. Второе число запишем в виде степени с основанием 2 и получим: 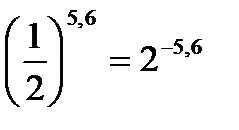 . Сначала сравним показатели степеней. Так как
. Сначала сравним показатели степеней. Так как 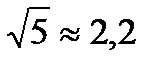 , то
, то 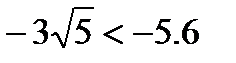 . Функция
. Функция 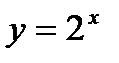 является возрастающей. Поэтому большему значению аргумента соответствует большее значение функции. Тогда имеем:
является возрастающей. Поэтому большему значению аргумента соответствует большее значение функции. Тогда имеем: 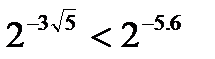 или
или 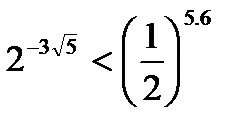 , т.е. второе число больше.
, т.е. второе число больше.



 2015-05-13
2015-05-13 4466
4466
