Из свойств логарифмической функции следует, что при любом 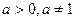 , и любом действительном значении
, и любом действительном значении 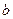 уравнение
уравнение 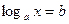 имеет и притом единственное решение
имеет и притом единственное решение 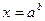 .
.
Уравнение 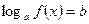 путем замены
путем замены 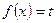 сводится к уравнению
сводится к уравнению 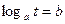 .
.
Уравнение 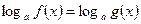
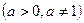 определено, если
определено, если 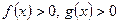 , и в области значений переменной, задаваемой этими условиями, равносильно уравнению
, и в области значений переменной, задаваемой этими условиями, равносильно уравнению 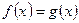 .
.
Заметим, что если значение 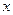 одновременно удовлетворяет уравнению
одновременно удовлетворяет уравнению 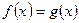 и одному из неравенств
и одному из неравенств 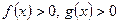 , то второе неравенство тоже выполняется, поэтому уравнение
, то второе неравенство тоже выполняется, поэтому уравнение 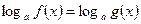 равносильно каждой из смешенных систем:
равносильно каждой из смешенных систем:
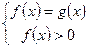 и
и 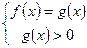
Обычно переходя от уравнения к смешанной системе, включают в нее то равенство, которое проще.
Пример 1. Решить уравнение 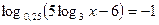
Решение. Уравнение равносильно каждому следующему:
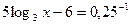
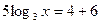
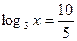
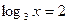
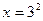
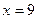
Ответ. 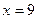 .
.
Пример 2. Решить уравнение 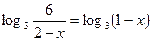 .
.
Решение.
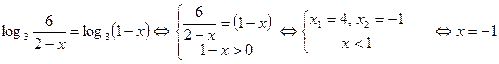
Ответ. 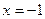 .
.
 2015-05-13
2015-05-13 382
382








