Пример 4. Решить уравнение 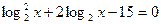 .
.
Решение. Положив 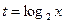 , получим уравнение
, получим уравнение
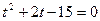
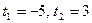
Если 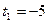 , то
, то 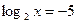 ,
, 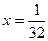 .
.
Если 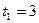 , то
, то 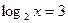 ,
, 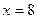 .
.
Ответ. 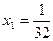 ,
, 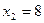 .
.
Логарифмические неравенства и методы их решения.
Решение простейших логарифмических неравенств.
Решение неравенств 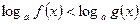
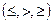
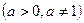 основано на свойстве монотонности логарифмической функции: если
основано на свойстве монотонности логарифмической функции: если 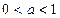 , то функция убывает, если
, то функция убывает, если 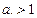 , то возрастает.
, то возрастает.
Если 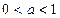 , то неравенство
, то неравенство 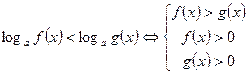 или
или 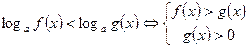
Если 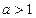 , то неравенство
, то неравенство 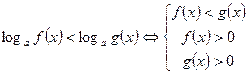 или
или 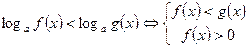 .
.
Решение неравенства 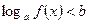 можно свести к решению неравенства
можно свести к решению неравенства 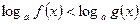 , представив число
, представив число 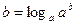

 2015-05-13
2015-05-13 4098
4098
