Метод главных компонент (МГК)

Пусть в примере (рис.1) имеется 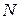рассматриваемых объектов, для каждого из которых определено значение четырех признаков. В четырехмерном графическом пространстве с осями координат 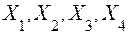это может быть представлено как облако из 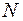точек. Если рассечь это четырехмерное пространство плоскостью, в которой находятся координатные оси, отвечающие признакам 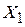и 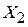, то в сечении окажется облако точек, которое в условиях взаимосвязи признаков 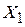и 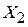друг с другом представляет собой эллипс рассеяния.

Если переменные стандартизированы (то есть, центрированы и нормированы) (2) центр этого эллипса рассеяния будет находиться в точке начала координат, как показано на рисунке 3.

Вследствие нормировки главная ось эллипса проходит через первый и третий квадрант при 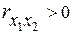, либо через второй и четвертый при 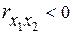. Форма этого эллипса (сжатость – вытянутость) будет определяться величиной коэффициента корреляции 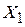с 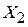, т.е. 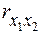, Чем больше 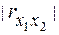, тем более вытянут эллипс и при 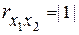он превращается в прямую линию, а при 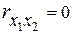- в круг. Проведем оси эллипса 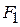и 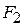. Ясно, что по мере увеличения 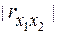происходит уменьшение степени разброса точек наблюдений вдоль одной оси эллипса (на рисунке – ось 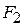) и увеличение разброса вдоль другой оси эллипса (на рисунке – ось ).

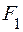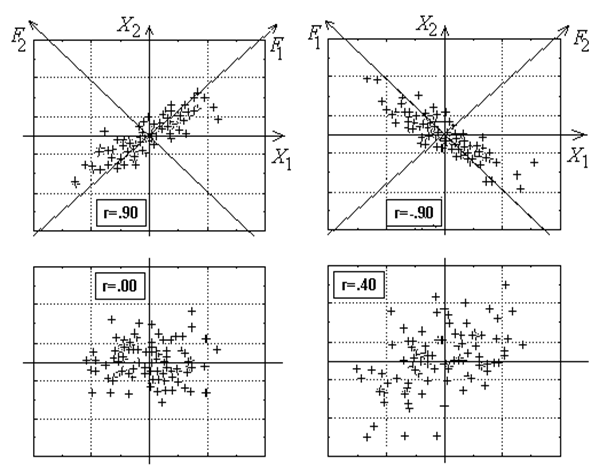
Рисунок 3

Если перейти от исходной координатной системы 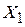, 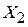к новой 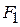, , 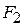оси которой ориентированы вдоль осей эллипса рассеяния, то очевидно, что в новой системе координат значения переменной 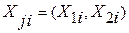вдоль оси 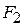будут иметь меньшую дисперсию, чем в исходной системе вдоль оси 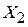, а значения этой переменной вдоль оси 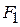, наоборот, будут иметь большую дисперсию, чем в исходной системе вдоль оси .

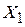Поэтому переменная 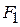несет в себе больше информации о выборке, чем 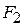. При этом, чем сильнее связаны между собой признак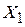и и 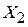, тем большим становится удельный вес той из новых переменных, которая ориентируется вдоль главной оси эллипса рассеяния.

Следовательно, в случае многомерного пространства появляется возможность ранжирования переменных (признаков) по их дисперсии в соответствии с их вкладом (значимостью) в общую характеристику изучаемого объекта, т.е. по уменьшению дисперсии значений признаков вдоль новых координатных осей .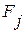

Можно предположить, что в многомерном пространстве облако точек выборочной многомерной совокупности по аналогии с рассмотренным выше двумерным случаем, представляет собой эллипсоид с несколькими разновеликими ортогональными осями. Поэтому в условиях взаимозависимости признаков для более компактного представления информации переходят к новой ортогональной системе координат (ориентированной по главным осям этого эллипсоида), которой отвечают новые переменные – главные компоненты 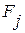( 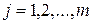и 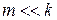). Они концентрируют в себе основную информацию об исходной выборке, что позволяет снизить размерность исходного признакового пространства (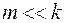). Эта процедура перехода к новой ортогональной системе координат (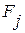) и составляет сущность метода главных компонент (МГК).

Указанный переход не затрагивает геометрической структуры взаимного расположения точек наблюдений 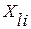. Характер их распределения сохраняется. Поэтому суммарная дисперсия остается прежней, т.е.

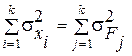(7)

(Рассматривается случай, когда число главных компонент равно числу наблюдаемых переменных).

Факторные нагрузки 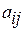в уравнениях (5)-(6) представляют собой коэффициенты корреляции между исходными 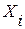и новыми 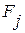переменными:

.

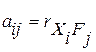Дисперсия случайных многомерных величин характеризуется ковариационной либо корреляционной матрицей.

Элементы ковариационной матрице являются ковариациями соответствующих переменных 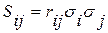( 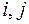– номера признаков (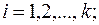 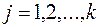)). На диагонали матрицы расположены дисперсии переменных.

Корреляционная матрица 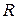содержит в качестве своих элементов линейные коэффициенты парной корреляции i –ого признака с j –тым признаком (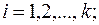 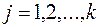). Диагональные элементы матрицы – дисперсии стандартизированных переменных равны 1.

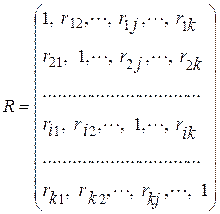. (8)

Суммарная дисперсия всей системы 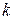-признаков в выборочной совокупности объема 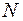равна сумме этих единиц, т.е. равна следу корреляционной матрицы .

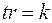Корреляционная матриц путем линейных преобразований может быть преобразована в диагональную, то есть матрицу, все значения которой, кроме диагональных, равны нулю. Превращение в нуль недиагональных членов означает, что признаки становятся независимыми друг от друга (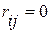 при 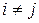). Но и в этих условиях суммарная дисперсия всей системы 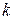-признаков в выборочной совокупности остается прежней. Однако её значение перераспределяется по 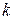-признакам.

Диагональные элементы полученной матрицы являются собственными значениями корреляционной матрицы 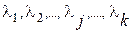. Эти собственные значения и есть величины дисперсии признаков 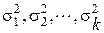в условиях, если бы признаки были бы независимыми друг от друга. Сумма этих собственных значений 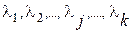равна следу корреляционной матрицы, т.е. 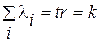, то есть количеству переменных.

Процедура нахождения значений этих дисперсий представляет собой нахождение собственных значений 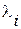корреляционной матрицы для каждого из 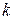-признаков. Корреляционную и диагональную матрицы связывает соотношение

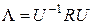, (9)

где 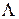- диагональная матрица, на главной диагонали которой находятся собственные числа 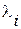корреляционной матрицы, 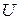- матрица, столбцы которой – собственные вектора корреляционной матрицы .

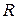Нормированный собственный вектор 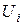равен

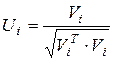(10)

В случае использования стандартизированных исходных данных вектор собственных значений будет нормирован изначально.

Собственные значения 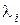могут быть найдены как корни характеристического уравнения

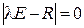(11)

Собственный вектор 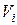, соответствующий собственному значению 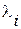корреляционной матрицы 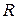, определяется как отличное от нуля решение уравнения

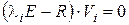(12)

Каждое собственное значение корреляционной матрицы соответствуют одной главной компоненте, а доля 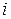-той компоненты в общей дисперсии может быть определена по формуле

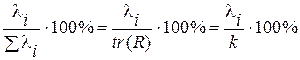(13)

Матрица факторных нагрузок 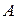содержит факторные нагрузки 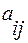для всех 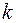-признаков и 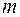-факторов и может быть определена как

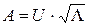, (14)

Факторные нагрузки изменяются от –1 до +1 и являются аналогом коэффициентов корреляции. В матрице факторных нагрузок необходимо выделить значимые и незначимые нагрузки с помощью критерия Стьюдента. Расчетное значение критерия определяют по формуле

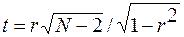. (15)

Проверку гипотезы о значимости факторной нагрузки осуществляют путям сравнения с критическим значением или путем нахождения наблюдаемого значения уровня значимости.

Сумма квадратов нагрузок 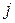-ой компоненты по всем наблюдаемым признакам равна собственному значению данного фактора 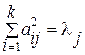. Тогда можно определить вклад 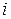-ой переменной в формировании 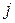-ой компоненты:

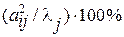. (15)

Вклад каждой из компонент в формировании значений того или иного признака составляет .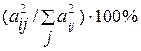

Сумма квадратов всех факторных нагрузок одной переменной на полный набор факторов по строке равна единице 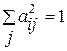, то есть полной дисперсии одной стандартизированной переменной, а сумма квадратов всех факторных нагрузок всех факторов по всем переменным равна суммарной дисперсии (т.е. следу или порядку корреляционной матрицы, или сумме её собственных значений).

.

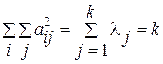Таким образом, общий вклад всех главных компонент в суммарную дисперсию равен 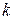. Тогда удельный вклад 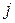-й главной компоненты определяется по формуле

.

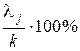Обычно для анализа используют 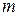первых главных компонент, вклад которых в суммарную дисперсию превышает 60—70%. Если главные компоненты упорядочены в порядке убывания, то суммарный вклад 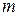первых главных компонент определяется из выражения

.

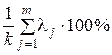Матрица факторных нагрузок А используется для смысловой интерпретации главных компонент, которые представляют собой линейные функции исходных признаков. Для интерпретации главных компонент используется лишь часть переменных, для которых |факторные нагрузки являются значимыми.

В общем виде факторная структура 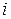–го признака представляется в форме 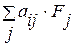, в которую включаются лишь значимые нагрузки. Матрицу значений главных компонент можно получить из формулы

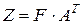
Используя матрицу факторных нагрузок можно вычислить значения всех факторов для каждого наблюдения исходной выборочной совокупности по формуле:

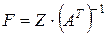, (15)

Вычисленные значения главных компонент широко используются для графического представления результатов факторного анализа.

По матрице факторных нагрузок может быть восстановлена корреляционная матрица: 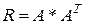. Восстановленные только по главным компонентам коэффициенты корреляции будут меньше исходных по абсолютной величине, а на диагонали будут не 1, а значения общностей.

Часть дисперсии переменной, объясняемая оставленными главными компонентами, называется общностью. Для каждой переменной общность может быть вычислена по формуле

,

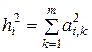где 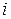- номер переменной, а 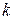-номер главной компоненты.