2015-05-13
237
Задача 4.1. К ободу однородного диска радиусом R = 0,2 м приложена касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения МТР = 98,1 Нм. Найти массу m дисков, если известно, что диск вращается с угловым ускорением e = 100 рад/с2.
  Дано:
R = 0,2 м
F = 98,1 Н
МТР = 98,1 Н∙м
e = 100 рад/с2
| Решение:
1.
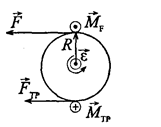Рисунок к задаче 4.1.
|
| Найти: m -? |
2.Уравнение вращательного движения диска в векторной форме согласно (4.7):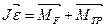 
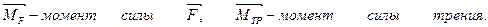
3.Выберем ось Х в направлении вектора углового ускорения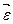 
(на нас, перпендикулярно плоскости чертежа).
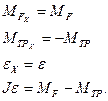4. ОХ:
5. Момент инерции диска: J= 1/2 mR2; MF = F R.
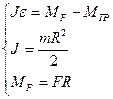6. Решая полученную систему уравнений:
можно получить: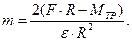 
Вычисления производим в Международной системе единиц СИ: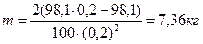 
Ответ: 7,36 кг.
Задача 4.2. Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через блок масcой m = 1 кг. Найти ускорение а, с которыми движутся гири, и силы натяжения Т1 И Т2 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
| Дано:
m1 = 2 кг
m2 = 1 кг
m = 1 кг
|
Решение:
1.
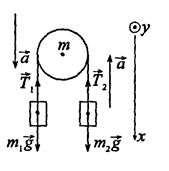Рисунок к задаче 4.2.
|
| Найти: а -? Т1 -? Т2 -? |
2. Запишем в векторной форме уравнения поступательного движения первой и второй гири: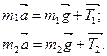 
|
|
|
и уравнение вращательного движения диска: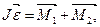 
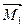- момент силы натяжения нити Т1, 
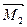- момент силы натяжения нити Т2.
3.Спроектируем первые два уравнения на ось ОХ, а последнее на ось ОУ и добавим уравнение кинематической связи.
4. Решая полученную систему уравнений: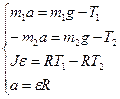 
можно получить: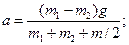 
Т1 = m1(g - a); T2 = m2g(g + a);
Вычисления делаем в Международной системе единиц СИ:
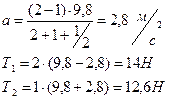
Ответ: 2,8 м/с2; 14 Н; 12,6 Н.
