2015-05-13
1213
Постановка задачи. Требуется добиться фиксированного значения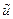 
функции полезности 
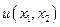при минимальных затратах 
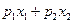на покупку двух товаров, одного – стоимостью 
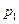за единицу, другого – стоимостью 
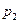за единицу измерения (предполагается, что можно купить любые количества 
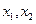этих товаров).
Задача сводится к поиску минимума функции 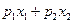при условии 
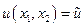. (29)
Функция Лагранжа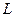 
имеет вид
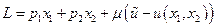(30).
Приравниваем нулю её частные производные по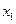 
, 
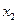и 
:
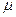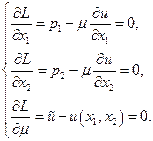(31).
Предполагаем, что система (31) имеет единственное решение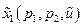 
, 
, 
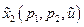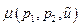. Функции 
, 
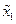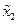называются функциями спроса по Хиксу, а функция
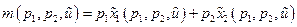(32)
называется функцией расходов.
Из первых двух равенств (31) для единственного решения , ,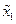 
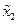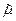получаем
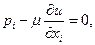
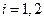. (33)
Утверждение. Имеет место равенство
.
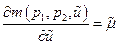► Из (32) и (33)следует
= 
◄
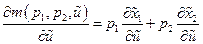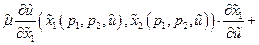
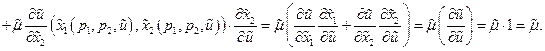Утверждение. (Шепард) Справедливы равенства
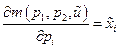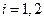, . (34)
► Из (32) и (33) получаем
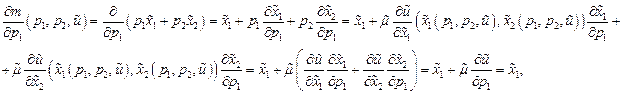т.к.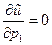 
.
Для 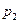равенство (34)устанавливается аналогично.◄
Рассмотрим пример, в котором в уравнении (29)
, 
, .
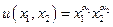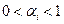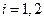Применим метод множителей Лагранжа и рассмотрим функцию Лагранжа
.
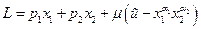Находим её частные производные и приравниваем их к нулю
|
|
|
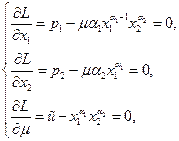(35)
а решение 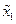, , 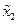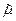этой системы удовлетворяет условиям
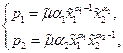
из которых находим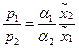 
или
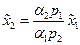. (36)
Тогда последнее из уравнений (35), вместе с (36), даёт
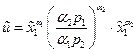, (37)
Откуда
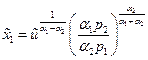, (38)
а из (36) и (38)находим
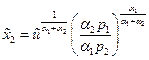. (39)
Функции (38) и(39)- это функции спроса по Хиксу.
Подставляя (38) и(39)в первое из равенств (35), находим
,
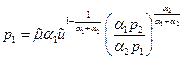откуда
.
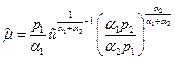Функция расходов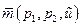 
, согласно (32), (38) и(39),имеет вид
.
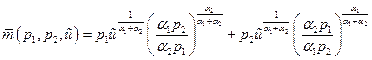Проверка того, что в точке 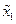, 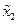функция 
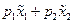имеет экстремум (минимум) сводится к исследованию второго дифференциала функции Лагранжа
.
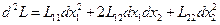Используя (30), получаем
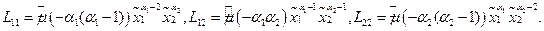
Кроме того, дифференцируя уравнение связи (т.е.(37)), находим
,
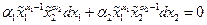т.е.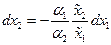 
. В итоге второй дифференциал функции Лагранжа равен 
.
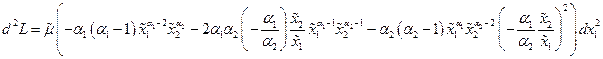Все слагаемые в скобках больше нуля ввиду условий 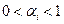, , 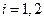поэтому в рассматриваемой точке, действительно, минимум.
Приложение. Понятие независимости функций
Иногда возникает вопрос, а нет ли среди уравнений связи лишних, которые являются следствиями остальных уравнений?
Для ответа на этот вопрос рассмотрим систему функций
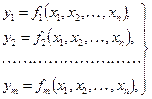(1)
определенных и непрерывных, вместе со своими частными производными, в некоторой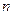 
-мерной открытой области 
.
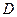Рассмотрим случай, когда значение одной из них, например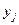 
, однозначно определяется совокупностью тех значений, которые принимают остальные функции
.
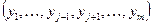Точнее говоря, если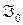 
есть множество таких 
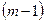-мерных точек, отвечающих всевозможным точкам 
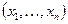в 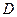, то предполагается что в 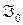будет иметь место функциональная зависимость
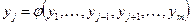, (2)
причем это равенство оказывается тождеством относительно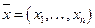 
в 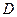, если вместо всех 
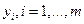, подставить функции (1). Тогда говорят, что в области 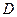функция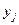 зависит от остальных. Для того, чтобы иметь возможность применять дифференциальное исчисление, мы включим в определение еще требование, чтобы функция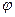 
была определена и непрерывна со своими частными производными в некоторой открытой области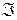 
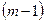-мерного пространства, содержащей множество .
|
|
|
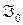Если, в частности, одна из функций (1), 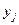, сводится к постоянной, то она будет зависеть от остальных: здесь можно просто положить 
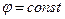. Вообще функции 
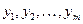называются зависимыми в области 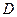, если одна из них (все равно какая) зависит от остальных.
Примеры. 1) Если положить
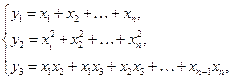
то нетрудно проверить, что во всем 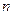-мерном пространстве будет выполняться тождество 
.
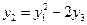Таким образом,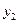 
зависит от 
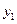и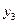 
.
Если ни в области 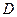, ни в какой-либо частичной, в ней содержащейся, области не имеет место тождество вида (2), то функции 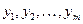называют независимыми в области .
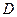Рассмотрим матрицу Якоби
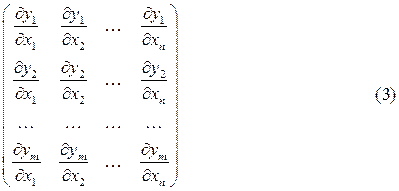
Предполагая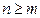 
, имеем такую теорему:
Теорема 1. Если хоть один определитель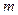 
-ого порядка, составленный из элементов матрицы (3), отличен от нуля в области 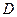, то в этой области функции 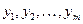независимы.
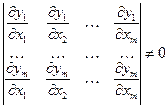. (4)
Замечание. Если бы не равным нулю был не этот, а какой-нибудь другой определитель, то, изменив нумерацию переменных, можно было бы свести вопрос к случаю (4).
►Доказательство теоремы будем вести от противного. Предположим, что одна из функций, например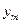 
, выражается через остальные, так что
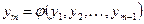, (5)
хотя бы в некоторой части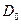 
области .
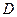Продифференцировав это тождество по каждой из переменных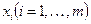 
, мы получим ряд тождеств (в 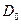) вида
.
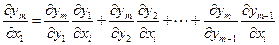
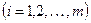Мы видим, что элементы последней строки определителя (5) получаются путем сложения соответственных элементов первых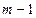 
строк, умноженных предварительно на множители 
, 
, 
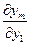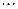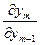. Такой определитель, как известно, равен нулю. Это противоречит условию теоремы. Полученное противоречие доказывает невозможность равенства (5).◄
