Метод наименьших квадратов

Наиболее простая модель парной регрессии соответствует случаю, когда функция f (x) в (1.1) является линейной, а случайная компонента входит аддитивным образом:

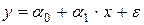, (1.2)

где a ₀, a ₁ – параметры модели. При этом классический случай такой модели предполагает, что случайная компонента удовлетворяет следующим требованиям:

· математическое ожидание e равно нулю: М [ e ]=0;

· дисперсия e постоянна по всему массиву наблюдений: D [ e ]=const;

· случайные остатк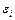и и 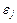, относящиеся к разным наблюдениям являются независимыми (взаимно некоррелированными), что может быть выражено равенствами: 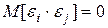при всех i ¹ j;

· случайные отклонения e не зависят от объясняющей переменной х;

· кроме того, обычно предполагают, что случайная компонента e распределена по нормальному закону.

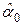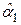Задача регрессионного анализа в данном случае сводится к отысканию наиболее приемлемых оценок и параметров уравнения a ₀ и a ₁ по известным выборочным значениям влияющей и результирующей переменных. Еще раз подчеркнем, что значения оценок 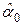и 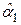не совпадают с истинными значениями a ₀ и a ₁, поскольку определяются на основании ограниченной и, возможно, не вполне достоверной выборки.

Оценка параметров производится обычно с помощью метода наименьших квадратов (МНК), суть которого сводится к отысканию значени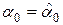й и 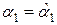, минимизирующих сумму квадратов отклонений фактических значений результирующей переменной от ее расчетных значений:

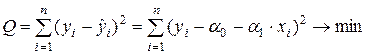(1.3)

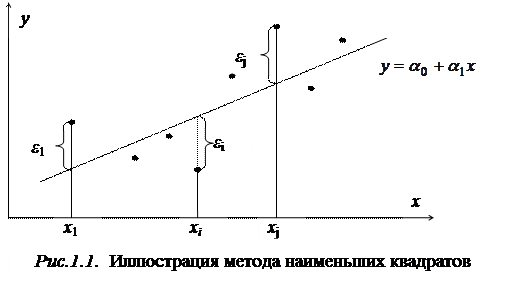
В случае парной регрессии МНК имеет наглядную геометрическую интерпретацию (рис.1.1). Параметры регрессионного уравнения a ₀ и a ₁ подбирают таким образом, чтобы прямая линия 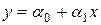прошла как можно ближе ко всем имеющимся точкам.

Численная реализация МНК сводится к решению задачи минимизации (1.3). Заметим, что в данном случае x_i и y_i – известные данные (числа), так что величина Q является функцией от двух переменных - параметров 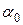и .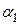

Воспользуемся необходимым условием экстремума функции нескольких переменных. Для этого найдем частные производные 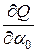, 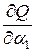и приравняем их к нулю:

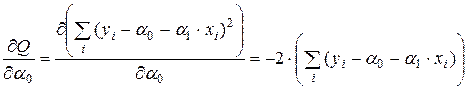
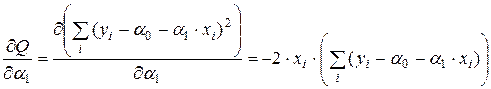
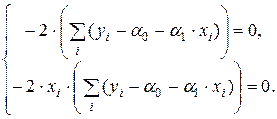
Отсюда после несложных преобразований получим следующую систему линейных уравнений:

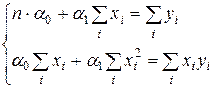(1.4)

где n – объем выборки. Систему (1.4) называют системой нормальных уравнений относительно оценок параметров парной линейной регрессии.

Решая данную систему, можно получить непосредственные формулы для расчета оценок параметров:

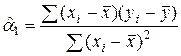или 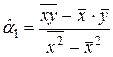, (1.5)

,

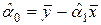где , , , .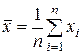

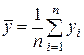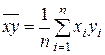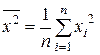Получаемые оценки параметров линейного уравнения парной регрессии имеют достаточно четкую экономическую или физическую интерпретацию. Оценка 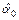показывает, какое среднее значение имеет результирующая переменная y при отсутствии влияния со стороны переменной x, а оценка 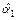определяет, на сколько в среднем меняется результирующая переменная при изменении переменной x на единицу.