2015-05-13
355
| i | xi | yi | xi 2 | xiyi |
| 25,7 | 660,49 | 1978,9 | ||
| 23,5 | 552,25 | |||
| 22,5 | 506,25 | |||
| i | xi | yi | xi 2 | xiyi |
| 21,1 | 445,21 | 2278,8 | ||
| 19,4 | 376,36 | 3511,4 | ||
| 19,7 | 388,09 | 2738,3 | ||
| 20,6 | 424,36 | |||
| 20,2 | 408,04 | 2363,4 | ||
| Σ | 242,7 | 5399,05 | 23923,8 |
Используя данные таблицы 1.1, запишем систему линейных уравнений вида (1.4):
.
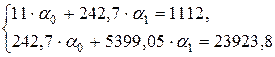Решая систему, определим оценки параметров уравнения парной линейной регрессии: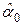 
=406,03 и 
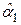=-13,82. Эти значения можно получить и воспользовавшись формулами (1.5). Таким образом, регрессионную зависимость между объемом продаж яблок и их ценой можно записать следующим образом:
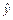=406,03-13,82× x
Используя данное уравнение, можно осуществлять точечный прогноз объема продаж в зависимости от установленной цены. Например, при x 0=26:
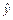= 406,03-13,82×26» 46,7 кг.
Отметим, что оценк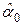и и 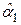параметров парной линейной регрессии, полученные на основе МНК, являются в некотором смысле статистически "идеальными" при условии выполнения исходных классических предпосылок. Это выражается в выполнении трех базовых свойств оценок:
|
|
|
cостоятельности, т. е.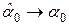 
и 
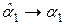при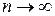 
(МНК-оценки параметров при неограниченном увеличении числа наблюдений стремятся к действительным (теоретическим) значениям этих параметров и, следовательно, становятся более надежными);
несмещенности, т. е.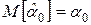 
, 
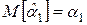(систематическая ошибка в определении линии регрессии отсутствует);
эффективности, т.е. эти оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.
