Cуть методов численного интегрирования

МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ

1. Суть методов численного интегрирования

2. Реализация методов в MS Excel

Cуть методов численного интегрирования

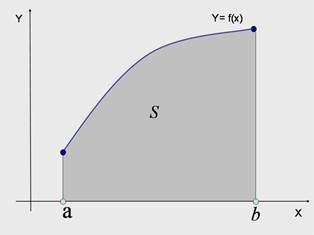Пусть функция у=f(x) (f(x)>0) непрерывна для хÎ [a,b], тогдаопределенный интеграл пропорционален площади криволинейной трапеции, образованной подынтегральной функцией на отрезке [a,b] и прямыми x=a, x=b

Идея численного интегрирования заключается в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто.

Разобьем отрезок [a, b] на n равных отрезков с шагом h,

x₀=a, x _i+1=x _i+h, y_i=f(x_i), i=0,1,2, ……,n-1.

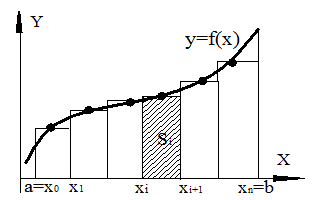Криволинейная трапеция соответственно разобьется на n элементарных криволинейных трапеций. Каждую ЭКТ заменяем фигурой, площадь которой вычисляется довольно просто и она равна S_i.

Сумму площадей всех этих ЭКТ назовем интегральной суммой:

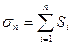(2.1)

Формула для приближенного вычисления интеграла (ФЧИ) имеет вид:

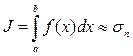(2.2)