Циклически повторяем следующую последовательность действий:
1. Строим равномерную сетку Wn, т.е. разбиваем отрезок интегрирования [a, b] на n равных отрезков с шагом h=(b-a)/n.
2. Находим интегральную сумму по формуле (2.1).
3. Повторяем пункты 1, 2 с шагом h/2 для 2n, т.е. строим сетку W2n и интегральную сумму (2.1). Получили два приближенных значения интеграла, две итерации.
4. Если две соседние итерации близки, т.е.
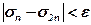 (2.3)
(2.3)
то за приближенное значение интеграла (1) с точностью e принимаем:
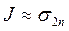 (2.4)
(2.4)
Если условие (2.3) не выполняется, то надо вернуться на пункт 3, т.е. еще раз уменьшить шаг вдвое и так до тех пор, пока условие (6) не будет выполнено.
Таким образом, можно записать формулы
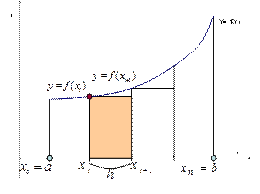
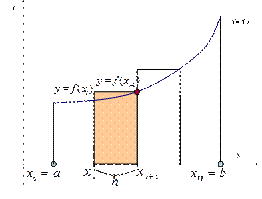
| для метода (левых) входящих прямоугольников | для метода (правых) выходящих прямоугольников | |
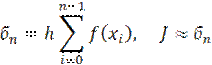
| 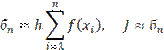
| |
| 
| |
| Следует заметить, что при вычислении суммы площадей фигур по методу входящих прямоугольников не учитывается последняя точка отрезка, а по методу выходящих прямоугольников – первая точка. | ||
| для метода средних прямоугольников | для метода трапеций | |
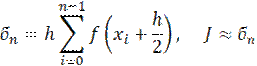
| ||
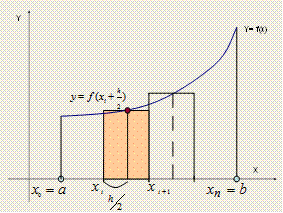
| 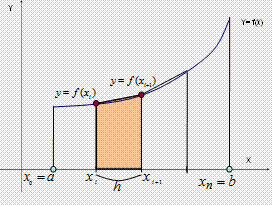
| |
Вычисления могут сопровождаться значительными погрешностями. Для снижения погрешности следует уменьшить шаг интегрирования (метод половинного шага), либо использовать более точные методы.
 2015-05-13
2015-05-13 657
657








