методу средних прямоугольников)

D29 =СУММ(С13:С21)*D9+(С12+С22)*D9/2 (т.е. формулу для вычисления площади фигуры по методу трапеций).

В данном случае не составляет труда найти точное значение этого интеграла, используя формулу Ньютона-Лейбница:

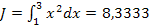и сравнить с полученными результатами.

Изменяя значения ячеек В6 (нижний предел интегрирования a), В7 (верхний предел интегрирования b), В8 (количество узлов n), С12 (формула подынтегральной функции f(x)) вы можете использовать эту таблицу для вычисления любого определенного интеграла с необходимой точностью.

Например. Увеличьте количество узлов, т.е. введите в ячейку В8 величину 20. Вычислив интегральные суммы, можно оценить точность вычисления интеграла

Если 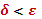, то итерационный процесс можно закончить.