Случайные величины

Литература: [6], гл. 4-9; [7], гл. 4-7, задачи 167, 177, 194, 211, 239, 240, 253, 255, 263, 268, 298, 316, 332, 341, 348, 376, 379, 401, 403; [4], гл. 8, §9.

Пример. Задана функция распределения случайной величины Х:

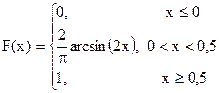
Необходимо найти плотность вероятности, математическое ожидание и дисперсию данной случайной величины. Также требуется определить вероятность попадания в отрезок [0,25; 1].

Решение. Плотность вероятности равна производной от функции распределения. Вычисляя производную, находим:

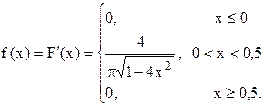
Математическое ожидание непрерывной случайной величины в общем случае равно

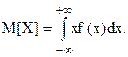
В поставленной задаче интегрируется кусочно-гладкая функция. Пределы интегрирования сужаются до интервала, в котором плотность вероятности не равна нулю. Кроме этого, в левой окрестности точки 0,5, плотность вероятности 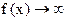, поэтому интеграл вычисляется как несобственный второго рода. Находим:

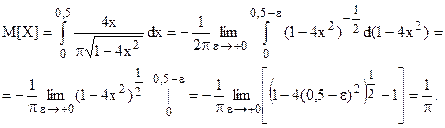
Согласно определению, дисперсия случайной величины Х равна

.

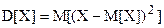На практике для вычисления дисперсии используют ее свойство, по которому .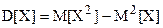

Математическое ожидание квадрата случайной величины Х также является несобственным интегралом второго рода:

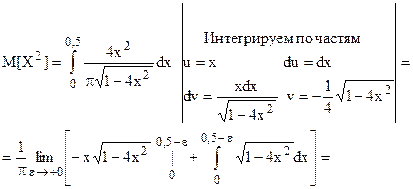
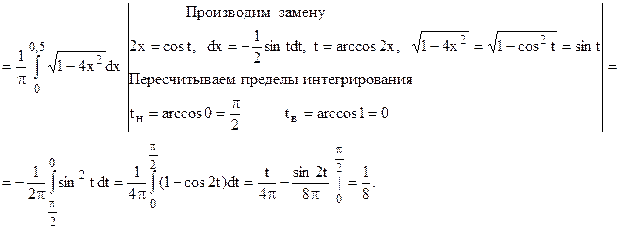Вычислим дисперсию случайной величины Х, используя представленную ранее формулу:

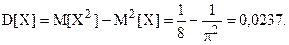
Для произвольной случайной величины Х справедливо, что вероятность

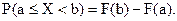
Для непрерывной случайной величины неравенство может быть строгим или нестрогим с обеих сторон. В нашем случае вероятность

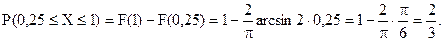
Вопросы для самопроверки.

1. Дайте определение случайной величины. Приведите примеры.

2. Дайте определение функции распределения случайной величины и докажите ее свойства.

3. Дайте определение плотности распределения и докажите ее свойства.

4. Приведите примеры случайных величин, которые подчиняются распределениям: гипергеометрическому, биномиальному, геометрическому и распределению Пуассона.

5. Приведите примеры случайных величин, которые подчиняются распределениям: равномерному, нормальному и показательному.

6. Как найти вероятность попадания случайной величины в заданный интервал, если она задана своей функцией распределения, плотностью распределения?

7. Как найти распределение функции от дискретной и непрерывной случайной величины?

8. Как найти вероятность попадания пары случайных величин в заданный прямоугольник?

9. Какие две случайные величины называются независимыми? Что представляет собой распределение суммы двух независимых случайных величин?

10. Дайте определение математического ожидания случайной величины и докажите его свойства.

11. Дайте определение дисперсии случайной величины и докажите ее свойства. Что называется среднеквадратичным отклонением случайной величины?

12. Что называется ковариацей двух случайных величин? Что называется коэффициентом корреляции? Докажите его свойства.

13. Докажите неравенство и теорему Чебышева.

14. Что называется характеристической функцией случайной величины? Докажите свойства характеристической функции.

15. Сформулируйте центральную предельную теорему и теорему Ляпунова.