2015-05-13
20816
Часто модель объекта управления представляет собой последовательную цепочку типовых звеньев, поэтому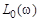 
можно получить, суммируя отдельные ЛАЧХ. Подобное суммирование позволяет предложить следующую процедуру построения .
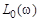На частоте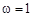 
(или в логарифмическом масштабе 
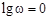) фиксируется точка, соответствующая значению 
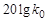, где 
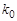– коэффициент усиления объекта.
На оси абсцисс отмечаются частоты сопряжения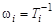 
(или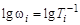 
), 
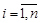, где n – число типовых звеньев в составе передаточной функции объекта.
До первой частоты сопряжения строится низкочастотная асимптота с наклоном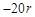 
дБ/дек., если 
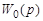содержит интегрирующие звенья, а r – число таких звеньев. Наклон характеристики будет равен 
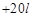дБ/дек., если передаточная функция объекта содержит дифференцирующие звенья, l – число этих звеньев. Низкочастотная асимптота строится таким образом, чтобы она сама или ее продолжение проходили через точку .
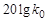На частотах сопряжения происходит «излом» асимптотической ЛАЧХ объекта. Наклон ЛАЧХ изменяется на 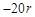дБ/дек., если соответствующая частоте сопряжения постоянная времени находится в знаменателе передаточной функции объекта, r – число таких звеньев.
«Излом» асимптотической ЛАЧХ будет равен 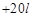дБ/дек., если постоянная времени находится в числителе передаточной функции, l – число звеньев. Новая асимптота проводится до следующей частоты сопряжения, где также происходит ее «излом» в соответствии с указанным правилом.
Пример 6.5
Построить асимптотическую ЛАЧХ объекта, передаточная функция которого имеет вид:
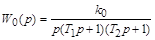
где коэффициент усиления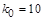 
, а постоянные времени 
, 
.
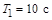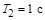Используем предложенную процедуру для построения ЛАЧХ объекта. Предварительно определим характерные точки:
,
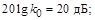
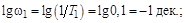
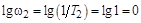отметим их на осях координат (рис. 6.9).
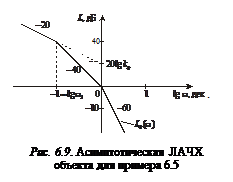
Построение ЛАЧХ начинается из области низких частот, которая расположена левее первой частоты сопряжения. Низкочастотная асимптота имеет наклон – 20дБ/дек., так как передаточная функция объекта содержит интегрирующее звено. Проводится она до частоты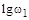 
так, чтобы ее продолжение пересекало ось ординат в точке 
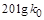. На частоте 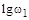происходит «излом» характеристики на –20дБ/дек., что соответствует апериодическому звену в составе 
.
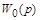До следующей частоты сопряжения (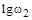
) асимптота имеет наклон – 40дБ/дек. «Излом» характеристики на частоте 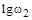равен – 20дБ/дек., так как в составе 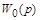есть апериодическое звено с постоянной времени 
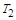. Следовательно, наклон последней асимптоты ЛАЧХ объекта будет равен – 60дБ/дек.
Для построения ЛАЧХ объекта с произвольной передаточной функцией:
.
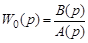следует перейти к выражению для частотной характеристики:
.
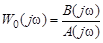Амплитудно-частотная характеристика определяется так:
,
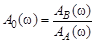что позволяет вычислить:
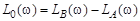. (6.35)
Таким образом, логарифмическая амплитудная частотная характеристика объекта находится как разность (6.35).
