Для непрерывной двумерной случайной величины плотность распределения имеет вид:
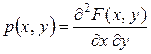
Свойства плотности распределения:
- p(x,y)≥0 – условие не отрицательности;
-
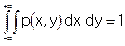 - условие нормировки;
- условие нормировки; -
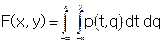
-
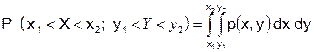
Плотности распределения составляющих
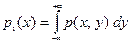 и
и 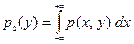
Законы распределения составляющих
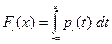 и
и 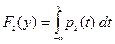
Случайные величины X и Y называются независимыми, если 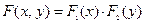 .
.
Для непрерывных величин 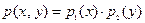
Математические ожидания и дисперсии составляющих системы двух дискретных случайных величин
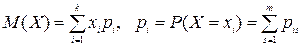 ,
, 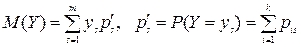
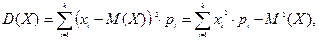
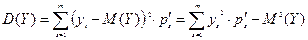
 2015-05-13
2015-05-13 369
369








