В узком смысле: понимается ряд теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
A) Неравенство Маркова
Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, т.е Р(Х≥0)=1. Тогда для любого δ>0 верно неравенство 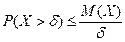 .
.
Т.к. события Х>δ и Х≤δ противоположные, то имеем другую форму: 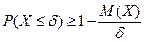
B) Неравенство Чебышева
Для любой случайной величины Х справедливо неравенство: 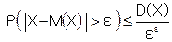 .
.
Учитывая, что события |X-M(X)|>ε и |X-M(X)|≤ε противоположны, то имеем другую форму: 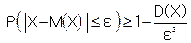 .
.
 2015-05-13
2015-05-13 332
332








