2015-05-13
412
Решить неоднородное линейное дифференциальное уравнение (НЛДУ), описывающее переходный процесс линейной АСР, находящейся на границе устойчивости (вынужденное «движение»). Построить график переходного процесса, выделяя в возмущенном «движении» вынужденные и свободные составляющие.
Передаточная функция системы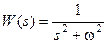 
(1).
Дифференциальное уравнение АСР, получаемое в результате обратного преобразования Лапласа для левой и правой части выражения (1)
:
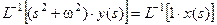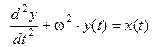(2)
Простой переходный процесс – это характеристический процесс линейной АСР или ее отдельного звена, исследуемый при подаче на вход АСР простого ступенчатого возмущения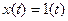 
. Подставим в правую часть выражения (2) :
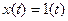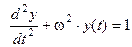(3).
Полученное выражение – есть выражение неоднородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами (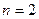
).
Общее решение этого уравнения можно представить как сумму общего решения соответствующего однородного уравнения (ОЛДУ) -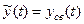 
и частного решения неоднородного уравнения (НЛДУ) - 
.
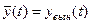Для нахождения общего решения ОЛДУ запишем характеристическое уравнение:
.
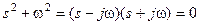Это уравнение имеет пару комплексно сопряженных корней -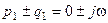 
. Зная корни характеристического уравнения, можно записать общее решение ОЛДУ:
.
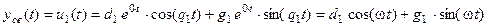Для нахождения частного решения представим функцию правой части в виде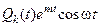 
:
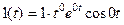, т.е. 
, 
, 
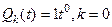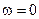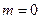. Комплексное число 
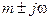, которое в нашем случае есть 
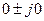не совпадает ни содним корнем характеристического уравнения. Следовательно, частное решение НЛДУ:
.
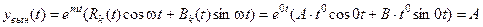Для определения значение постоянной А подставим полученное частное решение в дифференциальное уравнение (2):
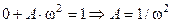, то есть 
.
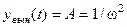Тогда общее решение НЛДУ, описывающее простой переходный процесс в АСР
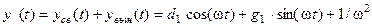. Значение коэффициентов 
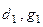должно быть найдено из начальных условий. Отметим, что в условии задачи не оговаривались начальные условия. Для решения НЛДУ, описывающего характеристический переходный процесс в линейной АСР, эти условия всегда нулевые по функции и всем актуальным для этого уравнения производным. Таков принцип анализа АСР в линейной теории автоматического регулирования, следующий из суперпозиции переходных процессов по отдельным возмущениям. Из нулевых начальных условий получаем
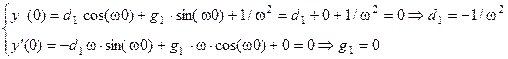
Таким образом, функция, описывающая простой переходный процесс в исследуемой АСР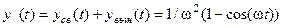 
, при этом функция, описывающая свободное движение - 
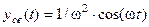, а функция, описывающая вынужденное движение - 
.
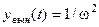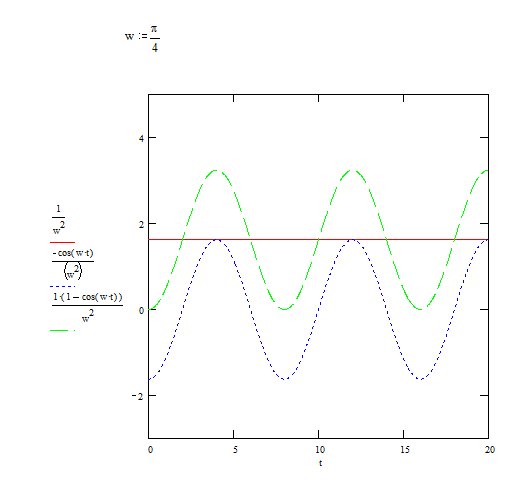
Переходный процесс, характерный для данной АСР имеет в своей структуре незатухающую гармонику, обусловленную парой чисто мнимых корней. В таких случаях говорят, что АСР находится на границе устойчивости. Построим график простого переходного процесса в данной АСР, выделяя свободную и вынужденную составляющую, для чего воспользуемся программой MATHCAD.
