Исследовать изменение во времени выходного расхода (переходный процесс) в системе «Емкость с самовыравниванием уровня» при ступенчатом изменении (возмущении) входного расхода.
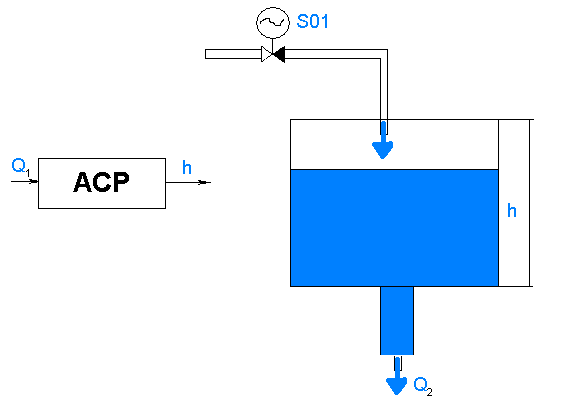
Рисунок к задаче 6.
До прихода возмущения в системе «Емкость с самовыравниванием уровня» самопроизвольно установилось равновесие, которое можно выразить условием равенства расходов на входе в емкость и выходе из емкости 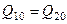 . Естественно, в состоянии равновесия уровень остается неизменным. Возмущенный расход опишем функцией
. Естественно, в состоянии равновесия уровень остается неизменным. Возмущенный расход опишем функцией 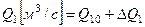 , где
, где 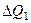 - ступенчатое возмущение. Изменение выходной переменной
- ступенчатое возмущение. Изменение выходной переменной 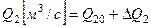 . Изменение расхода
. Изменение расхода 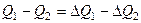 свяжем с изменением уровня:
свяжем с изменением уровня:
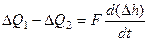 , где
, где 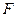 - площадь поперечного сечения бака,
- площадь поперечного сечения бака, 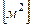 ,
, 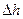 - изменение уровня в м.
- изменение уровня в м.
Выразим 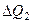 через изменение уровня (это и есть явление самовыравнивания!). Если
через изменение уровня (это и есть явление самовыравнивания!). Если 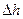 мало, то допустимо выражение
мало, то допустимо выражение 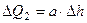 , где а – коэффициент, имеющий размерность
, где а – коэффициент, имеющий размерность 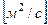 . Окончательно получим
. Окончательно получим 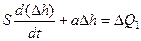 . Полученное уравнение есть НЛДУ первого порядка. Такое уравнение динамики имеют типовые звенья, именуемые в теории автоматического управления апериодическими. Решим его относительно
. Полученное уравнение есть НЛДУ первого порядка. Такое уравнение динамики имеют типовые звенья, именуемые в теории автоматического управления апериодическими. Решим его относительно 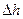 .
.
Характеристическое уравнение 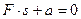 имеет единственный действительный отрицательный корень -
имеет единственный действительный отрицательный корень - 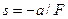 . Следовательно, общее решение ОЛДУ:
. Следовательно, общее решение ОЛДУ: 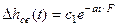 . Частное решение НЛДУ
. Частное решение НЛДУ 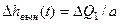 . Таким образом получили функцию, описывающую переходный процесс:
. Таким образом получили функцию, описывающую переходный процесс: 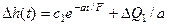 .
.
Определим значение неизвестной постоянной из начального условия: 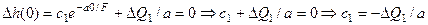 . Окончательно получим:
. Окончательно получим: 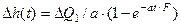
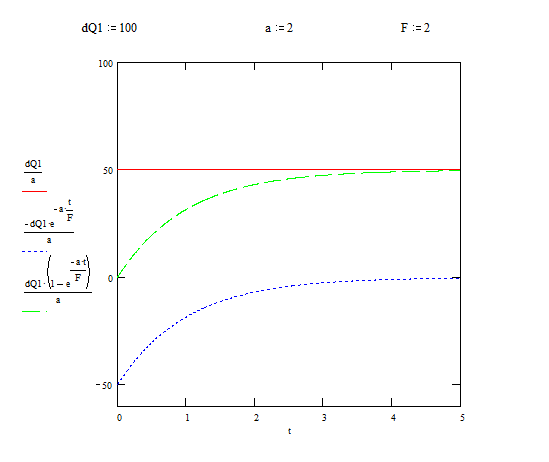
Построим график простого переходного процесса в данной АСР, выделяя свободную и вынужденную составляющую, для чего воспользуемся программой MATHCAD.
 2015-05-13
2015-05-13 534
534








