С источниками синусоидального напряжения

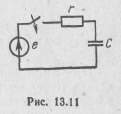
Особенности методики анализа переходных процессов в нераз­ветвленных цепях первого порядка с источниками синусоидаль­ного напряжения рассмотрим на примере цепи rC при подключе­нии ее к источнику синусоидального напряже­ния 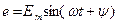(рис. 13.11).

В соответствии со вторым законом Кирх­гофа для рассматриваемой цепи можно запи­сать 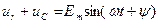. Учитывая, что 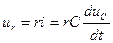, получим

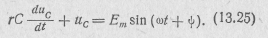
Свободная составляющая напряжения на емкости, являю­щаяся решением уравнения (13.25) без правой части, имеет вид

где p₁ = —1/rС — корень характеристического уравнения цепи

rСр+1 = 0.

Обозначив 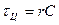, получим

Принужденная составляющая напряжения на емкости будет синусоидальной функцией времени:

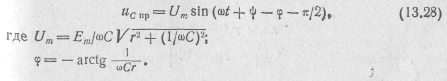
При этом общее решение уравнения (13.25) будет иметь вид

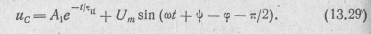
Постоянную интегрирования A₁ найдем из начальных условий 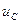(0)=0. Подставив это в выражение (13.29), при t=0 получим 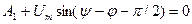, откуда .

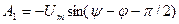При этом получим

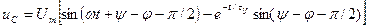. (13.30)

Из этого выражения видно, что переходные процессы врассматривае­мой цепи зависят от начальной фазы синусоидального напряжения ψ.

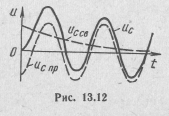
При ψ=φ±π/2 вцепи сразу наступает установившийся режим без переходного процесса.

При ψ=φ свободное напряжение на емкости будет максималь­ным (рис. 13.12), аследовательно, и переходный процесс вцепи будет более продолжительным.