К источнику постоянного напряжения

При подключении цепи rLC к источнику постоянного напряжения (рис. 13.18) дифференциальное уравнение для напряжения на емкости будет отличаться от уравнения (13.41) тем, что в правой

части этого уравнения в рассматриваемом случае будет не нуль, a :

Так как в рассматриваемом случае принужденная составляю­щая напряжения на емкости , а свободная составляющая, как и в предыдущем случае, определяется вы­ражением (13.43), то общее решение уравнения (13.60) будет иметь вид

· (13.61)

Подставив сюда начальное значение напря­жения на емкости и_с(0)=0, при t = 0 получим

A.+A₂ = -E. (13.62)

Взяв производную от выражения (13.61) и использовав второе начальное условие i (0)=0, при t=0 получим второе уравнение для определения постоянных интегрирования

р₁А₁+р₂А₂=0. (13.63)

Из системы уравнений (13.62) и (13.63) найдем:

Подставив это в формулу (13.61), получим

При.этом ток в цепи и напряжение на индуктивности будут из­меняться по законам:

Характер переходного процесса в рассматриваемой цепи, так же как и в предыдущем случае, будет зависеть от вида корней характеристического уравнения и может быть апериодическим (рис. 13.19) либо колебательным (рис. 13.20). В последнем случае

напряжение на емкости может достигать величины, равной почти удвоенному значению напряжения источника, подключаемого к цепи.

13.4.3. Подключение цепи rLC

к источнику синусоидального напряжения

Если к цепи rLC (см. рис. 13.18) вместо источника постоянного напряжения Е подключить источник синусоидального напряжения е=Е_т sin(ω t +ψ), то дифференциальное уравнение цепи (13.60) будет иметь вид

Принужденная составляющая решения этого уравнения равна напряжению на емкости в установившемся режиме:

Ограничившись рассмотрением случая колебательного харак­тера переходных процессов, для свободной составляющей в соот­ветствии с выражением (13.55) можем записать

,

где А и θ — постоянные интегрирования.

При этом общее решение уравнения (13.67) будет иметь вид

. (13.68)

Ток в цепи

Для высокодобротного контура, настроенного на частоту источ­ника подключаемого к контуру напряжения, можно считать, что , и . При этом, пренебрегая первым слагаемым в квалоатных скобках в выражении для тока, получим

Считая, что начальные условия в цепи являются нулевыми, из выражений ( 13.68) и (13.69) получим два уравнения для опреде­ления постоянных интегрирования:

из которых следует, что и

Подставив это в формулы (13.68) и (13.69),при 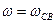по­лучим:

где I_т = ωСU_Ст.

График напряжения на емкости для рассматриваемого случая, когда 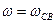, получившего название изохронизма, показан на

рис. 13.21. Амплитуда напряжения на емкости нарастает по за­кону , асимптотически приближаясь к значению, равному амплитуде этого напряжения в установившемся режиме. Анало­гичным образом изменяется и амплитуда тока в цепи. Длитель­ность переходного процесса определяется коэффициентом затуха­ния б. Чем больше б, тем быстрее заканчивается переходный про­цесс. Так как

то чем больше добротность контура Q, тем меньше δ, а следова­тельно, тем больше длительность переходного процесса в колеба­тельном контуре, а из обратно пропорциональной зависимости между шириной полосы пропускания колебательного контура и его добротностью следует, что длительность переходного процесса в контуре обратно пропорциональна ширине его полосы пропу­скания.

В случае если частота ω источника напряжения не точно со­впадает с частотой свободных колебаний в контуре , напря­жение на емкости и ток в цепи будут представлять собой суммы двух колебаний с разными частотами, амплитуда одного из кото­рых убывает по экспоненциальному закону. При этом возникают биения, частота которых равна разности частот ω и (рис. 13.22).

13.5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ