Пример 20.1

Найти реактивный двухполюсник, сопротивление которого задано в виде реактацрной функции

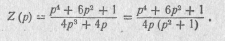
Решение.

В том, что заданная функция действительно является реактансной, нетрудно убедиться, определив ее нули и полюсы. Все они находятся на мнимой оси, яв­ляются простыми и взаимно чередуются. Так как заданная функция имеет по-

люсы ρ= 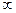, р =0 и р = ±j, то разложение этой функции иа элементарные дроби имеет вид

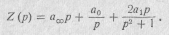
Коэффициенты разложения:

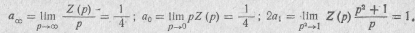
Подставив эти коэффициенты в Z(p), получим

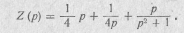
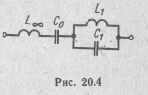
Схема двухполюсника приведена на рис. 20.4. Параметры нормированных элементов двухполюсиика:

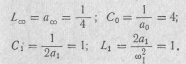
Рассмотренный выше способ реализации реактансных функций можно считать доказательством не только необходимости, но и до­статочности условий, которым должны удовлетворять операторные входные функ­ции реактивных двухполюсников, так как по этим условиям можно построить соответ­ствующую цепь.

Если разлагать на элементарные дроби операторные проводимости, являющиеся функциями, обратными функциям оператор­ных сопротивлений, то получим еще четыре схемы реактивных двухполюсников.

Пусть, например, операторная проводимость имеет вид

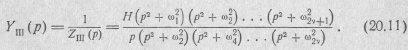
Учитывая, что это выражение совпадает с выражением (20.8) для Z_1V(p), можно написать разложение:

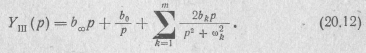
Первое слагаемое в этом выражении можно рассматривать как операторную проводимость емкости 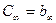(рис. 20.5,б), а вто­рое слагаемое — как операторную проводимость индуктивности L₀=l/b₀.

Слагаемое 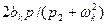представим в виде

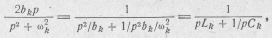
откуда следует, что это слагаемое можно рассматривать как опера­торную проводимость последовательного контура, состоящего из индуктивности L_k= 1 /2b_k и емкости C_k= 2 b_k / .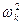

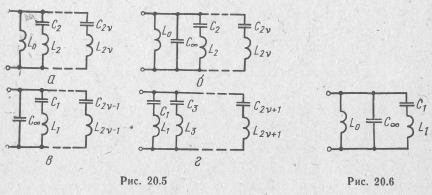
Таким образом, выражение (20.12) можно рассматривать как операторную проводимость двухполюсника, состоящего из парал­лельно включенных емкости 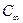, индуктивности l₀, и последова­тельных контуров, состоящих из индуктивностей L_k и емкостей C_k (см. рис. 20.5, б). Па этом же рисунке приведены еще три разно­видности схем реактивных двухполюсников.

Пример 20.2.

Найти реактивный двухполюсник, проводимость которого задана в виде реактансной функции

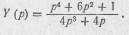
Решение.

Используя результаты предыдущего примера, получим

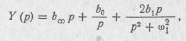
где .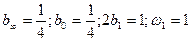

Подставив это в разложение для К(р), получим

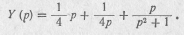
Параметры элементов двухполюсника:

.

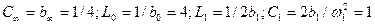Схема двухполюсника приведена на рис. 20.6.

Из выражений (20.9) и (20.12) следует, что сумма любого числа реактансных функций является также реактансной функцией и что любую сложную реактансную функцию можно представить в виде суммы двух более простых реактансных функций.

В частности, реактансную функцию Z(p) сполюсом при р= 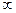можно представить суммой:

Z(p) = 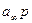+ Z₁(p), (20.13)

где α 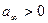, a Z ₁ (p) — реактансная функция с нулем при р= .

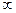Реактансную функцию Z(p) с полюсом при ρ = 0 можно пред­ставить в виде

Z(p) = a₀/p + Z ₁ (p), (20.14)

где а₀>0, a Z_l(p) — реактансная функция с нулем при p=0.