В виде цепной дроби

Представление реактансных функций Z(p) и Υ(ρ) в виде цеп­ной дроби осуществляется путем последовательного выделения полюсов этих функций при p= 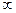или при p= 0.

Пусть функция Z(p) имеет полюс при р= . Тогда, располо­жив полиномы числителя и знаменателя Z(p) по убывающим сте­пеням и деля числитель на знаменатель, получим

Z(p)=pL ₁ + Z ₁ (P).

Здесь L₁>0, а функция Z ₁ (p) согласно формуле (20.13) яв­ляется также реактансной функцией, обращающейся в нуль при р= .

Слагаемое pL ₁реализуется в виде индуктивности L ₁(рис. 20.7,а). Так как функция Z₁(p) имеет нуль при р= 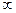, то функция Υ(p) = 1 /Z(p) имеет здесь полюс. Выделяя этот полюс путем деления знаменателя Z ₁ (p) на его числитель, получим

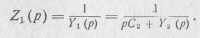
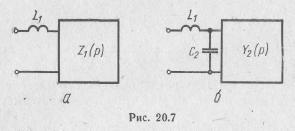
Здесь С₂>0, а функция Y₂(р) является реактансной функ­цией, обращающейся в нуль при p= .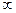

Слагаемое рС₂ реализуется в виде емкости С₂, включенной па­раллельно с проводимостью Y₂(р) (рис. 20.7,6),

Подставив Z ₁ (p) в выражение для Z(p), получим

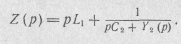
Продолжая этот процесс последовательного выделения полю­сов Z(p) и Υ(р) при p= , получим цепную дробь вида

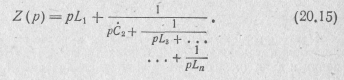
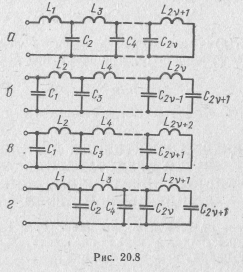
Ута дробь реализуется в виде схемы реактивного двухполюс­ника, приведенной на рис. 20.8, а.

Если функция Z(p) имеет нуль при p = , то, разлагая в цеп­ную дробь функцию Υ(p)= ₁ /Z(p) путем последовательного выделения полюсов при p= 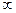, получим схему двухполюсника, приведенную на рис. 20.8, б.

Если при выделении полюсов функций Z(p) и У(р) при р= 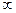полиномы числителей и знаменателей этих функций расположить по возрастающим степеням р, то получим еще две разновидности схем реактивных двухполюсников (рис. 20.8,6 и г),

Пример 20.3.

Наши реактивный двухполюсник, сопротивление Которого задано реактансной функцией

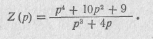
Решение.

Путем последовательного деления числителя Z(p) на знаменатель, знаме­нателя на первый остаток и т. д. представим заданную функцию в виде цепной дроби

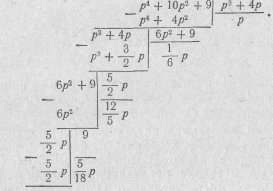
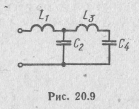
Искомая цепная дробь будет иметь вид

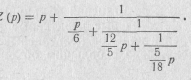
Этой дроби соответствует двухполюсник, схема которого приведена на рис. 20.9, где .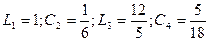

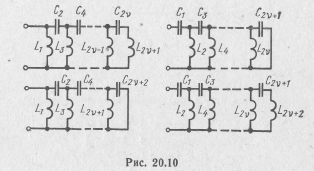
При выделении из реактансных функций Z(p) и Y(р) полюсов при p=0 получим цепную дробь вида

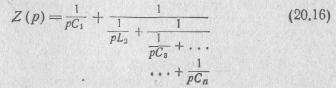
и еще четыре разновидности схем реактансных двухполюсников (рис. 20.10).

Двухполюсники, схемы которых приведены на рис. 20.8—20.10, обычно называют двухполюсниками лестничного типа.

Все рассмотренные в настоящем и предыдущем подразделах двухполюсники характерны тем, что из всех возможных схем двух­полюсников, соответствующих заданным реактансньш функциям,

они содержат наименьшее число элементов, равное наивысшей сте­пени р заданных функций. Схемы этих двухполюсников обычно называют каноническими схемами.

Таким образом, любую заданную реактансную функцию можно реализовать в виде четырех канонических схем (см. рис. 20.2, 20.5, 20.8 и 20.10), которые являются эквивалентными. Если применять комбинированную методику реализации, то количество эквива­лентных схем может быть увеличено. Однако получающиеся при этом схемы уже не будут каноническими.

Если нули и полюсы реактансной функции заранее неизвестны, то проще находятся лестничные реактивные двухполюснцки, так как вычисление нулей и полюсов реактансных функций при боль­шом их порядке сопряжено с большим объемом вычислительной работы.

20.5. РЕАЛИЗАЦИЯ ДВУХПОЛЮСНИКОВ ТИПА rС

При синтезе двухполюсников типа rС воспользуемся результа­тами, полученными при рассмотрении синтеза двухполюсников типа LC. Для этого установим связь между операторными вход­ными функциями этих двухполюсников.

В выражениях для операторного входного сопротивления Z(p)=Δ_z/Δ₁₁ и операторной входной проводимости Υ(p)= 1 /Z(p) = Δ₁₁/Δ_Z цепи rC элементами определителя контурны

уравнений Δ_Z и его алгебраических дополнений Δ₁₁ является опе­раторное сопротивление

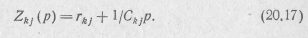
Произведя в этом выражении замену p=s², получим

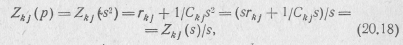
где

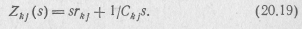
Так как множитель 1/s входит во все элементы Δ и Δ₁₁, то для цепи, состоящей из п контуров, получим

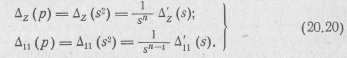
Элементами Δ' (s) и 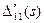является сопротивление Z_kj(s) (20.19), которое можно рассматривать как сопротивление цепи LC, считая, что r_kj = L_kj и s=p. При этом для входных операторных сопротивлений двухполюсника типа rС получим

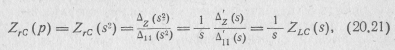
где z_lc(s) — входное операторное сопротивление двухполюсника

типа LC.

Из этого выражения видно, что если входное операторное со­противление двухполюсника типа LC, взятое как функция s, раз­делить на оператор s и заменить s² на р, то получим входное опе­раторное сопротивление двухполюсника типа rC. Так, например, произведя указанные операции с входным операторным сопротив­лением двухполюсника типа LC, определяемым выражением (20.8),

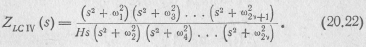
получим

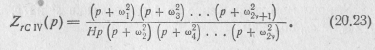
Аналогичным образом из входных операторных сопротивлений двухполюсника типа LC, определяемых выражениями (20.5) —

(20.7), можно получить еще три вида входных операторных сопро­тивлений двухполюсника типа rС:

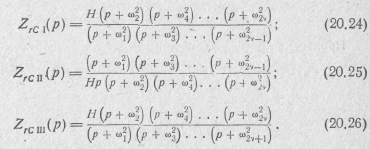
Учитывая чередуемость ω_k, из выражений (20.23) — (20.26) можно установить следующие особенности входных операторных сопротивлений двухполюсников типа rС:

а ) высшая степень полинома числителя на единицу меньше или равна степени полинома знаменателя;

б) все полюсы и нули расположены на вещественной отрица­тельной полуоси, являются простыми и взаимно чередуются, при­чем ближайшим к началу координат является полюс (он может, в частности, находиться и в начале координат); полюса в беско­нечности быть не может.

Из выражений, обратных уравнениям (20.23) — (20.26), можно установить следующие особенности входных операторных проводи-мостей двухполюсников типа rС:

а) высшая степень полинома числителя на единицу больше или равна степени полинома знаменателя;

б) все полюсы и нули расположены на вещественной отрица­тельной полуоси, являются простыми и взаимно чередуются, при­чем ближайшим к началу координат является нуль.

Установленная выше связь между входными операторными функциями двухполюсников типа rС и LC позволяет при синтезе двухполюсников типа rС использовать рассмотренные ранее ме­тоды синтеза двухполюсников типа LC.

Для разложения функции Z_rC(p) (20.23) на простые дроби воспользуемся выражением (20.9), которое запишем в виде

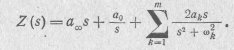
Умножив это выражение на 1/S и заменив s² на р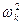_, на σ _k и 2a_k на a_k, получим

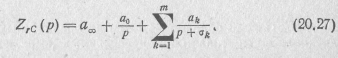
Коэффициенты этого выражения 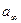, a ₀ и a_k, являющиеся ве­щественными положительными числами, можно определить по формулам:

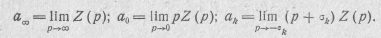
Первое слагаемое выражения (20.27), соответствующее значе­нию функции Z_rC(p) при p = 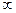, можно реализовать в виде актив­ного сопротивления 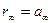, второе слагаемое, соответствующее

полюсу функции при p=0,— в виде емкости C₀= 1 /a₀, а каждое из слагаемых a_k /(p+σ _k), соответствующих полюсам функции при р=- σ _k,— в виде цепи, состоящей из параллельного соединения элементов r_k и C_k. Для определения величин r_k и C_k представим a_k/(p+ σ _k) в виде

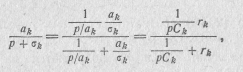
откуда следует, что C_k= l /a_k и r_k=a_k/ σ _k.

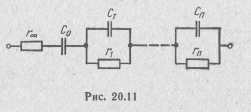
Схема двухполюсника, соответствующего выражению (20.27), приведена на рис. 20.11.

Для получения разложения функции Y_rC(р) на простые дроби вначале учтем, что в соответствии с формулой (20.21) эту функ­цию можно представить в виде

Y_rC(p) = sY_LC(s). (20.28)

В соответствии с уравнением (20.12) это выражение предста­вим в виде

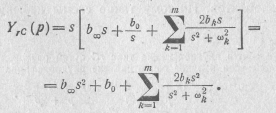
Заменив в этом выражении s² на p, 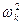на а_k и 2b_k на b_k, по­лучим

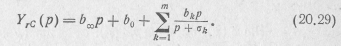
Коэффициенты этого выражения 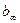, b₀ и b_k можно определить по формулам:

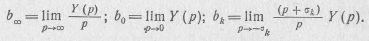
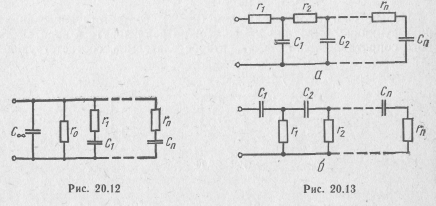
Выражению (20.29) соответствует схема двухполюсника, при­веденная на рис. 20.12, где ; r₀= l/ b ₀; C_k = b_k / σ_k; r_k = 1/ b_k.

Значения величин C_k и r_k получаются из представления b_kp/(р+ σ_k) в виде

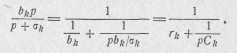
По аналогии с двухполюсниками типа LC можно получить еще два вида схем двухполюсников типа rС (рис. 20.13) путем разло­жения заданной функции сопротивления Z_rC(p) или проводимо­сти Y_rC(p) в непрерывную дробь, начиная деление с высших или низших степеней р.

Следует отметить, что все четыре рассмотренные схемы двух­полюсников типа rС содержат одинаковое, минимально возмож­ное число элементов. Поэтому такие схемы называют каноническими.

Пример 20.4.

Произвести синтез двухполюсника типа rC путем разложения Z_rc(p) в не­прерывную дробь, если входное сопротивление двухполюсника имеет вид

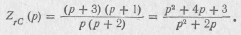
Решение.

Начнем деление числителя на знаменатель, расположив полиномы числителя и знаменателя по убывающим степеням:

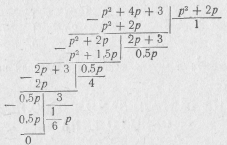
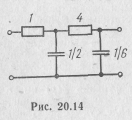
Отсюда видно, что Z_rC(p) можно представить в виде непрерывной дроби

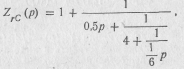
которой соответствует схема двухполюсника, приведенная на рис. 20.14.

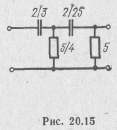
Если полиномы числителя и знаменателя расположить по возрастающим степеням, то получим

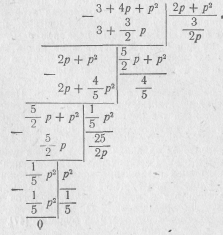
откуда видно, что Z_rC(p) можно представить в виде непрерывной дроби

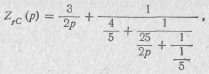
которой соответствует схема двухполюсника, приведенная на рис. 20.15.