2015-05-13
22107
В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание.
Для обоих случаев одномерного потока (прямолинейно–параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта.
Рассмотрим пласт толщиной h и длиной L Рис. 3.5. Слева, за границей нефтяного пласта, находится законтурная вода. Из пласта происходит отбор нефти с постоянным расходом Qo. Вода и нефть считается несжимаемыми. В законтурной области водонасыщенность равна единице, а в нефтяном пласте додонасыщенность равна остаточной водонасыщенности sво. Необходимо рассчитать распределение водонасыщенности с различные моменты времени.
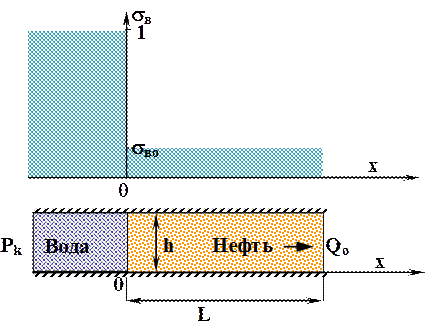 Рис. 3.5. Схема пласта и начальное распределение водонасыщенности |
Эта задача иписывается уравнениями неразрывности:
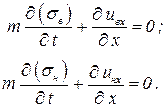 | (3.22) |
И обобщенным законом Дарси:
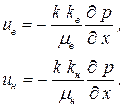 . | (3.23) |
Сложим уравнения неразрывности. Сумма насыщенностей равна единице, поэтому:
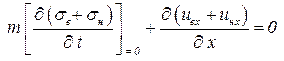 . | (3.24) |
При интегрировании последнего уравнения учтем, что жидкости несжимаемые, поэтому расход отбора нефти равен расходу закачки воды. При плоско параллельном движении будут равны и скорости. Обозначим скорость внедрения воды через uo = Qo/(B h).
Тогда:
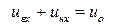 . | (3.25) |
Подставим скорости фильтрации, найденные из обобщенного закона Дарси в последнее уравнение:
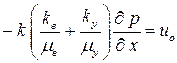 . | (3.26) |
Найдем из последнего уравнения градиент давления и подставим его в обобщенного закона Дарси для воды:
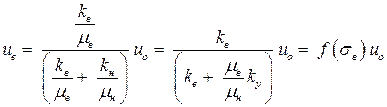 . | (3.27) |
Здесь через f(sв) обозначена функция Баклея - Леверетта
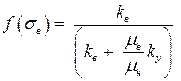 . | (3.28) |
Функция Баклея—Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту. Задачи повышения нефте – и газоконденсатоотдачи в значительной степени сворятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции Баклея – Леверетта в направлении увеличения полноты вытеснения.
Типичные графики функции Баклея – Леверетта и ее производной f'(sв) изображены на рис. 3.6. С ростом насыщенности f(sв) монотонно возрастает от 0 до 1. Характерной особенностью графика f(sв) является наличие точки перегиба, участков вогнутости и выпуклости, где вторая производная f ''(sв) соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта.
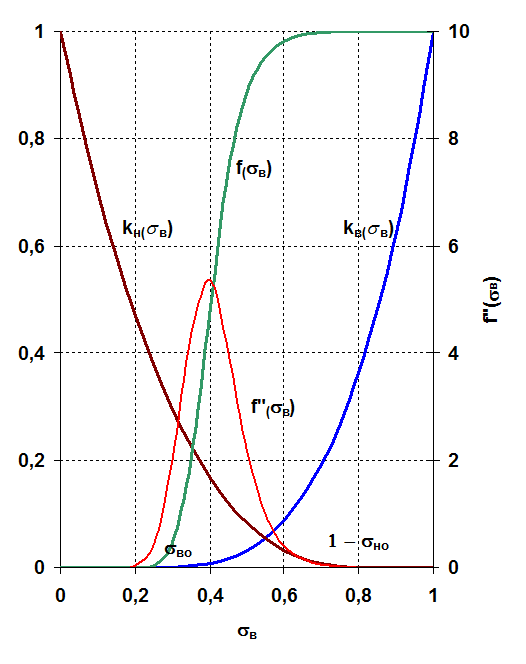 Рис. 3.6. Типичные графики функции Баклея - Леверетта и ее производной |
Для нахождения распределения водонасыщенности по пласту подставим скорость фильтрации воды (3.26) в уравнение неразрывности для воды:
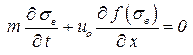 . | (3.29) |
Считая, что водонасыщенность зависит от координаты x, получим:
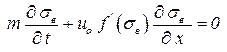 . | (3.30) |
где f '(sв) – производная от функции Баклея – Леверетта по водонасыщенности.
Решение этого уравнения первого порядка в частных производных имеет вид:
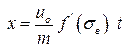 . | (3.31) |
Это решение математически справедливо рис. 3.7, но физически выполняется не для всех значений насыщенности. Из рисунка видно, что в каждой точке пласта будут три значения насыщенности, что абсурдно.
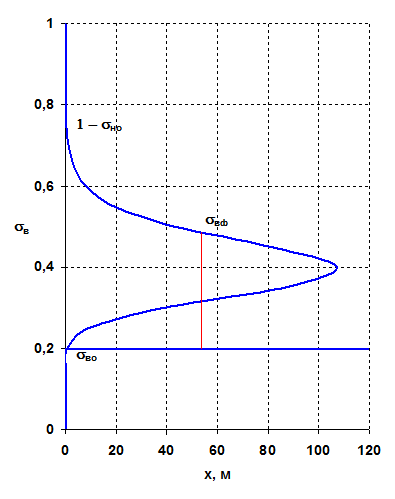 Рис. 3.7. Распределение водонасыщенности по длине пласта |
Физической особенностью модели двухфазного вытеснения Бакалея - Леверетта является зависимость скорости фильтрации воды от значения насыщенности. Действительно, из формулы (3.27) и графика зависимости функции Бакалея – Леверетта от водонасыщенности следует рисунок 3.7, что с ростом водонасыщенности скорость фильтрации воды сначала растёт, а потом уменьшается.
