Задание для самостоятельной работы. 1. Вычислить значение производной в произвольной точке x=x0 аналитически и численно тремя методами для пяти значений приращения аргумента Δx=1; 0.2; 0.1

1. Вычислить значение производной в произвольной точке x=x₀ аналитически и численно тремя методами для пяти значений приращения аргумента Δ x =1; 0.2; 0.1; 0.01; 0.001. Результаты расчета вывести на экран и распечатать в виде таблицы

Таблица вывода результатов расчета:

Δx	y(x)	y'(x)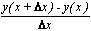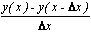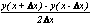
0.2
0.1
0.01
0.001

Варианты функций:

Вар.	Вид функции	Вар.	Вид функции
	x(t)=Ae-at sin(ωt+b)		y=ctgm (ax)
	x(t)=Aeat cos(ωt+b)		y(x)=(eax-e-ax)n
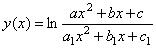			x(t)=tat
	уυ(t)=cos2(at+b)		y(x)=(ax)sin(bx)
	yυ(t)=sin2(at+b)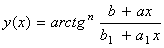
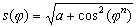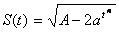	q(t)=(a-btn)n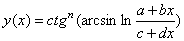
	y(x)=xncos(ax)		R(φ)=arccosm(a+bφn)
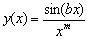			r(φ)=csin(aφ+b)
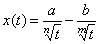			y(x)=ln(tgn(ax+b))
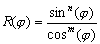			vυ(t)=loga(tn+bm)k
	S(φ)=Вcоsn(aφ+b)		S(φ)=Asinn(aφ+b)
	y=tgax(x/a)		X(t)=lg(atn+b)

Примечание. Значение параметров a, b, c, d, m, n, A, B выбрать самостоятельно.