Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма 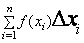 при стремлении всех промежутков ∆xi к нулю:
при стремлении всех промежутков ∆xi к нулю:
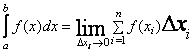 .
.
При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: 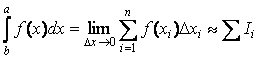 , где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
, где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
1. Приближенные формулы для вычисления интеграла методом прямоугольников (рис 12.1).
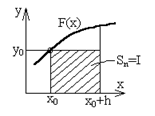
Рис. 12.1 - вычисление интеграла методом прямоугольников
Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника
 , где h - шаг интегрирования, у0 - значение функции в точке х=х0
, где h - шаг интегрирования, у0 - значение функции в точке х=х0
у(х0)=у0
2. Приближенные формулы для вычисления интеграла методом трапеций (рис. 12.2).
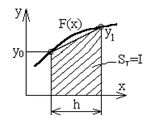
Рис. 12.2. - вычисление интеграла методом трапеций
Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной суммы как площадь трапеции
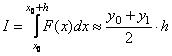
3. Приближенные формулы для вычисления интеграла методом Симпсона (рис. 12.3).
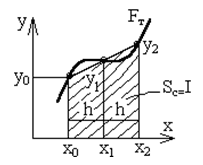
Рис. 12.3. - вычисление интеграла методом Симпсона
Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде: y(x)=y0A0(x)+y1A1(x)+y2A2(x), где:
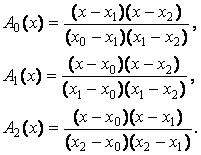
При x0=0; x1=h; x2=2h, получим:


При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид:
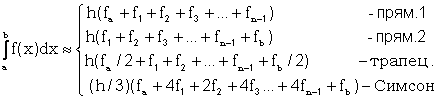 ,
,
где h - шаг по x, fa, fi, fb - значения функции при x равном a, xi, b соответственно.
Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a, b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников (рис. 12.4).
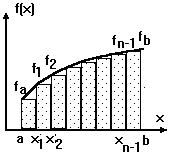
Рис. 12.4 - суть метода прямоугольников для отрезка [a, b]
 2015-05-13
2015-05-13 522
522








