Пусть дано дифференциальное уравнение первого порядка 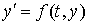 . Требуется найти функцию
. Требуется найти функцию 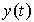 , удовлетворяющую при
, удовлетворяющую при 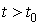 дифференциальному уравнению и при
дифференциальному уравнению и при 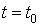 начальному условию
начальному условию 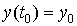 .
.
Теорема существования и единственности задачи Коши. Пусть функция 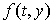 определена и непрерывна на множестве точек:
определена и непрерывна на множестве точек:
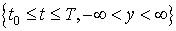 .
.
Предположим также, что она удовлетворяет условию Липшица: 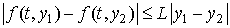 , для всех
, для всех 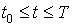 и произвольных
и произвольных 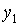 ,
, 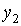 ,
,
где 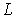 - некоторая константа (постоянная Липшица).
- некоторая константа (постоянная Липшица).
Тогда для каждого начального значения 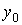 существует единственное решение
существует единственное решение 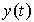 задачи Коши, определенное на отрезке
задачи Коши, определенное на отрезке 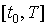 .
.
Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку 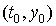 .
.
 2015-05-13
2015-05-13 2005
2005







