2015-05-13
609
Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.
Численно и аналитически найти:
a. закон движения материальной точки на пружине х(t),
b. закон изменения силы тока I(t) в колебательном контуре (RLC - цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.
Варианты заданий
Таблица режимов:
| № | Режим |
| Свободные незатухающие колебания | |
| Затухающее колебательное движение | |
| Апериодическое движение | |
| Предельное апериодическое движение | |
| Вынужденное колебание без сопротивления | |
| Вынужденное колебание без сопротивления, явление резонанса | |
| Вынужденное колебание с линейным сопротивлением | |
| Вынужденное колебание с линейным сопротивлением, явление резонанса |
Варианты заданий и номера режимов:
1. движение точк;
2. RLC – цепь.
| Вар. | Задание | Вар. | Задание |
| а) 1,2,5 | б)1,2,6 | ||
| а) 1,3,6 | а) 1,4,7 | ||
| б)1,3,7 | б)1,2,7 | ||
| а) 1,4,8 | а) 1,2,5 | ||
| б)1,2,8 | б)1,4,6 | ||
| а) 1,4,7 | а) 1,3,5 | ||
| б)1,3,6 | б)1,3,8 | ||
| а) 1,4,5 | б)1,4,5 | ||
| б)1,3,8 | а) 1,3,6 | ||
| а) 1,3,5 | б)1,4,7 | ||
| б)1,4,6 | а) 1,2,8 | ||
| а) 1,2,7 | б)1,4,8 | ||
| б)1,2,5 | а) 1,3,6 | ||
| а) 1,2,6 | б)1,3,7 | ||
| б)1,4,7 | а) 1,2,5 |
Рассмотрим более подробно порядок составления дифференциальных уравнений и приведения их к машинному виду для описания движения тела на пружине и RLC-цепи.
|
|
|
a. Движение материальной точки на пружине.
При выполнении этого задания необходимо рассмотреть движение материальной точки массой m на пружине (рис. 14.1) жесткостью c в среде с линейным сопротивлением под действием синусоидальной вынуждающей силы по горизонтальной поверхности.
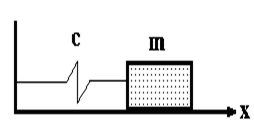
Рис. 14.1 - движение материальной точки на пружине
Уравнение движения (второй закон Ньютона) для материальной точки с учетом действия сил линейного сопротивления (-βx'), упругости пружины (-cx) и синусоидальной силы F0∙sin(pt) может быть записано следующим образом:
,
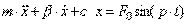где m=1+int(n/2) - масса материальной точки, β - коэффициент сопротивления, с=2+int(n/3) - жесткость пружины, х - координата (х=0 в положении равновесия точки), t - время, p - частота вынужденных колебаний, F0=n - амплитуда силы, n - номер варианта, int - целая часть числа. Параметры β, p и начальные условия выбираются самостоятельно с учетом рассматриваемого режима.
b. Колебательный контур (RLC цепь) (рис. 14.2):
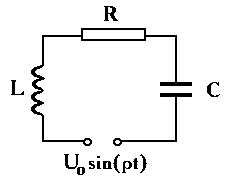
Рис. 14.2. - колебательный контур (RLC цепь)
Уравнение падения напряжения в цепи переменного тока имеет вид
,
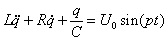где L=1+int(n/2) - индуктивность, R - сопротивление, C=2+int(n/3) - емкость конденсатора, q - заряд, U0=n-амплитуда напряжения, p - частота,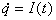 
- сила тока. Параметры R, p и начальные условия выбираются самостоятельно с учетом рассматриваемого режима.
|
|
|
