2015-05-13
919
В предыдущем пункте было описано дискретное преобразование Фурье - сопоставление набору значений функции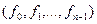 
набора коэффициентов 
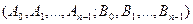. Процесс этого сопоставления в некоторых случаях можно ускорить, специальным образом организовав соответствующие суммирования.
Обратимся, для определенности, к формуле (15.9). Предположим, что число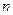 
является составным, т.е. 
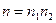при натуральных 
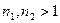. Разделим с остатком число 
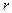на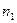 
и число 
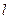(индекс суммирования) на 
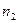; получим: 
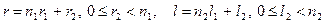. Заметим, что в образовавшихся обозначениях суммирование по 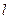эквивалентное повторному суммированию по схеме:
;
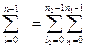преобразуем теперь суммируемое выражение:
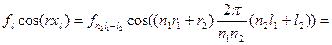
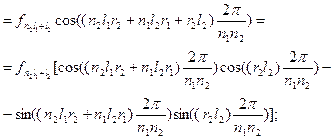
введем обозначения:
;
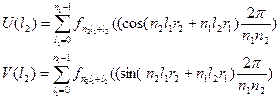тогда выражение (15.10) представляется в виде:
.
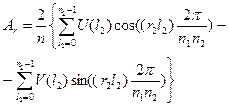Совершенно аналогично можно провести рассуждения с коэффициентом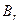 
, в результате чего снова возникнут те же 
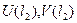; в итоге получится:
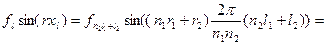
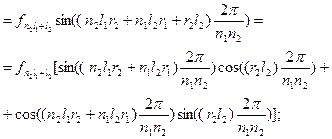
отсюда возникает соотношение:
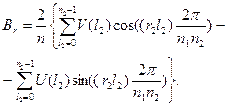
Отсюда возникает иная возможность вычисления дискретного преобразования Фурье, отличная от прямого вычисления: надо сначала найти выражения 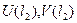, а затем уже сами числа 
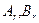; потребуется, как нетрудно заметить, меньше арифметических операций. Отсюда и название - «Быстрое преобразование Фурье».
