2015-05-13
1704
Типичная задача, описывающая теплоперенос вдоль одномерного стержня единичной длинны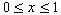 
при заданном начальном распределении температуры от (x) и заданных температурных режимах на концах стержня y (t), f (t) ставится следующим образом:
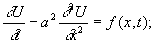t >0, 0 £ x £ 1;
U(0,x)=j (x)
U(t,0)=y (t); U(t,1)=f (t); (16.1)
Эта модельная задача является смешанной, так как содержит начальные (при t =0) и краевые условия (при x= 0 и x= 1). Она описывает различные диссипативные процессы (типа теплопроводности или диффузии) в твердых телах, газах, плазме, в магнитной гидродинамике, в биологии и т.д.
Областью решения задачи (16.1) будет являться полуполоса t >0, 0 £ x £ 1. Путем замены переменных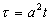 
дифференциальное уравнение приводится к виду:
поэтому избавимся от множителя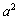 
, считая его равным 
единице. Тогда задача запишется в виде:
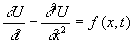0 £ t £ T, 0 £ x £ 1;
U(0,x)=j (x);
U(t,0)=y (t); U(t,1)=f (t);
Наложим на область 0 £ t £ T, 0 £ x £ 1 сетку образованную прямыми параллельными осям координат с шагом по x равным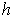 
, и шагом по t равным 
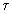, т.е. 
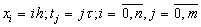где n и m количество линий сетки. Введем обозначения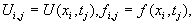 
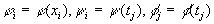и заменим производную по длине центральным разностным отношением:
|
|
|
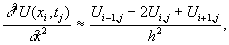(16.2)
а производную по времени правым конечно-разностным отношением:
.
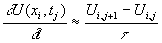Подставив эти выражения в дифференциальное уравнение получим конечно-разностное уравнение справедливое для всех внутренних узлов сетки:
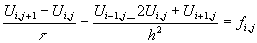
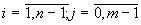(16.3)
Начальные и краевые условия дадут следующие уравнения:
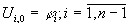(16.4)
.
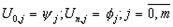Таким образом, задача (16.2) сводится к системе линейных уравнений (16.3) (16.4), решив которую можно получить значения искомой функции в узлах сетки.
Конфигурация узлов, значения сеточной функции в которых определяют вид разностных уравнений, записываемых для внутренних точек сетки, называется шаблоном разностной схемы. Для схемы (3) шаблон связывает одну точку слоя (временного)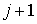 
с тремя точками слоя 
.
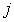Введем обозначение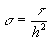 
и решим уравнение (3) относительно 
:
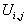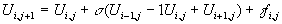
и пользуясь этим уравнением и значениями в начальных и граничных точках последовательно восстанавливать значения искомой функции в узлах сетки от слоя к слою, поэтому схема (3) называется явной.
Если заменить производную по времени левым конечно разностным уравнением:
,
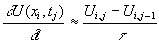то получим неявную схему связывающую три точки слоя j с одной точкой предыдущего слоя j- 1:
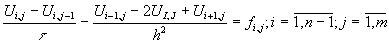(16.5)
,
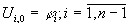
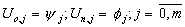Получаемая система линейных уравнений не эквивалентна системе с треугольной матрицей как при использовании явной схемы и для ее решения используется специальный прием позволяющий разделить систему на некоторое число систем меньшей размерности.
Рассмотрим точки первого слоя с номерами i=1, n-1. Поскольку значения искомой функции на предыдущем слое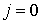 
известны из начальных условий для каждой точки этого слоя получим уравнение связывающее три неизвестных, причем в крайних точках слоя значения функции известны из граничных условий, т.е. получаем систему уравнений с трехдиагональной матрицей решить которую можно методом прогонки. Затем, используя это решение можно найти значения функции на следующем слое и так далее.
|
|
|
При решении задач с частными производными особенно актуальным становится вопрос об устойчивости конечно-разностных схем. Пусть конечно-разностная схема с некоторым шагом h (скалярным или векторным) записывается в виде некоторого конечно-разностного оператора:
,
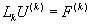где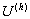 
- совокупность значений искомой функции в узлах сетки;
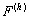- совокупность значений правой части дифференциального уравнения в узлах сетки.
Определение. Решение полученное с помощью схемы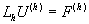 
называется устойчивым если для любого e >0 найдется ограничение шага 
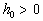, такое что решение возмущенной задачи с ограниченным возмущением:
; 
,
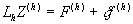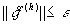будет не сильно отклоняться от решения исходной задачи:
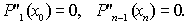
при любых значениях шага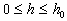 
и константе C не зависящей от шага h.
Устойчивость явной схемы (16.3) зависит от соотношения шагов h и t, при выполнении условия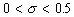 
эта схема будет устойчивой, в противном случае, т.е. при 
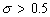явная схема перестает быть устойчивой. Неявная схема (16.5) устойчива при любом выборе шагов.
