Всякий элемент n-мерного линейного пространства можно представить, притом единственным образом, как линейную комбинацию векторов базиса.
Доказательство. Пусть ē1, ē2, …, ēn - базис линейного пространства L. Рассмотрим любой вектор ā 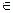 L. Тогда система векторов ē1,…, ēn, ā - линейно зависимая, то есть λ1ē1+…+ λnēn+ λn+1 ā=0, причем λn+1≠0.
L. Тогда система векторов ē1,…, ēn, ā - линейно зависимая, то есть λ1ē1+…+ λnēn+ λn+1 ā=0, причем λn+1≠0.
Если λn+1 =0, тогда 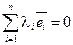 и какое-то из λi≠0
и какое-то из λi≠0 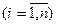
Это означает: ē1, ē2, …, ēn - линейно зависимы, что противоречит условию: ē1, ē2, …, ēn - базис, то есть линейно независимая система векторов.
Итак, λn+1≠0, тогда 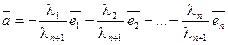 , то есть
, то есть
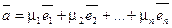 , где
, где 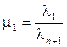 .
.
Таким образом, показали, что любой вектор можно представить как линейную комбинацию векторов базиса.
Покажем, что такое разложение единственно. Предположим, что наряду с полученным разложением ā по базису 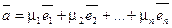 , существует другое
, существует другое 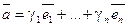 .
.
Вычитая, находим 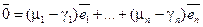 .
.
Так как векторы ē1, ē2, …, ēn - линейно независимы, то последнее равенство имеет место только тогда, когда 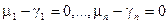 .
.
Таким образом, μi=γi для 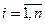 , а следовательно, разложение вектора по базису единственно.
, а следовательно, разложение вектора по базису единственно.
Всякий базис линейного пространства, векторы которого берутся в определенной последовательности, называют системой координат, а числа - коэффициенты в разложении любого вектора ā по базису - называют координатами вектора ā.
ā=x1 ē1+…+xnēn,
где х1,…., хn - координаты вектора ā.
Последнее выражение называют формулой разложения вектора по базису.
В общем случае при изменении базиса, координаты вектора изменяются.
Вектор можно задавать с помощью координат ā=(x1,x2,…,xn).
Рассмотрим два вектора:
ā=(x1,x2,…,xn) и 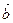 =(γ1, γ2, …, γn).
=(γ1, γ2, …, γn).
Используя определение линейного пространства, покажите что:
1) при сложении векторов их соответствующие координаты складываются:
ā+ 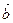 = (x1+γ1, x2+γ2, …, xn+γn);
= (x1+γ1, x2+γ2, …, xn+γn);
2) при умножении вектора на скаляр λ, каждая координата умножается на это число: λ ā=(λx1, λx2, …, λxn).
 2015-05-13
2015-05-13 9572
9572
