Определение линейного пространства

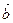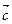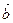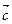
Пусть ā, , - элементы некоторого множества ā, , 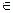L и λ, μ - действительные числа, λ, μ 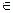R..

Множество L называется линейным или векторным пространством, если определены две операции:

1⁰. Сложение. Каждой паре элементов этого множества поставлен в соответствие элемент того же множества, называемый их суммой

ā + =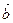

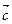
2°. Умножение на число. Любому действительному числу λ и элементу ā 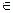L ставится в соответствие элемент того же множества λ ā 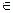L и выполняются следующие свойства:

1. ā+ 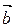= 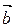+ ā;

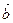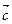2. ā+( + )=(ā+ )+ ;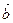

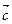3. существует нулевой элемент 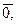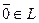, такой, что 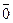ā + = ā;

4. существует противоположный элемент - 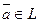такой, что ā +(- ā)= .

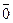Если λ, μ - действительные числа, то:

5. λ(μ, ā)= λ μ ā;

6. 1 ā= ā;

7. λ(ā + 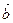)= λ ā+λ ;

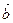8. (λ+μ) ā=λ ā +μā

Элементы линейного пространства ā, 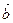, 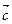... называют векторами.

Упражнение. Покажите самостоятельно, что данные множества образуют линейные пространства:

1) Множество геометрических векторов на плоскости;

2) Множество геометрических векторов в трехмерном пространстве;

3) Множество многочленов некоторой степени;

4) Множество матриц одинаковой размерности.