2015-05-13
485
Линейной комбинацией векторов ā 1 , ā 2, …, ān 
L называется вектор того же пространства вида:
,
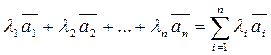где λ i - действительные числа.
Векторы ā 1,.., ān называются линейно независимыми, если их линейная комбинация будет нулевым вектором в том и только в том случае, когда все λ i равны нулю, то есть
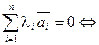λ i =0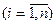 
Если же линейная комбинация будет нулевым вектором и хотя бы один из λi отличен от нуля, то эти векторы называются линейно-зависимыми. Последнее означает, что хотя бы один из векторов может быть представлен как линейная комбинация других векторов. Действительно, пусть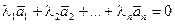 
и, например, 
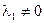. тогда, 
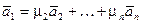, где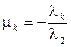 
.
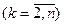Максимально линейно-независимая упорядоченная система векторов называется базисом пространства L. Число векторов базиса называется размерностью пространства.
Допустим, что существует n линейно-независимых векторов, тогда пространство называют n -мерным. Другие векторы пространства могут быть представлены как линейная комбинация n векторов базиса. За базис n- мерного пространства можно взять любые n линейно-независимых векторов этого пространства.
|
|
|
Пример 17. Найти базис и размерность данных линейных пространств:
а) множества векторов, лежащих на прямой (коллинеарных некоторой прямой)
б) множество векторов, принадлежащих плоскости
в) множество векторов трёхмерного пространства
г) множество многочленов степени не выше второй.
