Векторное произведение в координатной форме

Пусть известны координаты векторов 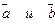, то есть

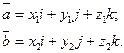
Используя свойства векторного произведения, найдем:

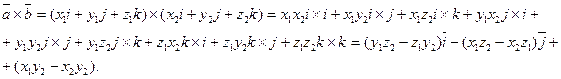
Выражения в скобках можно записать с помощью определителей второго порядка (проверьте), то есть:

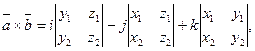
правую часть последнего выражения можно записать с помощью определителя третьего порядка:

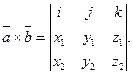
Эта формула является удобной записью векторного произведения в координатах.

Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

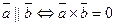
Из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах 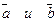, равна модулю векторного произведения:

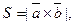
в частности, площадь треугольника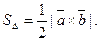

Одним из физических приложений векторного произведения является нахождение момента силы, возникающего при вращении твердого тела, закрепленного в некоторой точке А, под действием силы 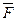, приложенной в точке В:

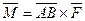
Пример 20. Найти площадь треугольника АВС, где А (-2, 1, 0);

В (3,4, 8); С (-1,3,6).