Смешанное произведение векторов

При последовательном умножении трех векторов 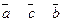возможны следующие случаи:

1) 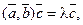где λ - скаляр,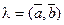

2) 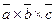- двойное векторное произведение, в результате получим вектор;

3) 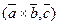- векторно-скалярное произведение, в результате получим число.

Смешанным произведением трех векторов называется их векторно-скалярное произведение, обозначают:

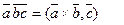
Найдем выражение смешанного произведения через координаты.

Пусть 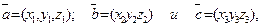тогда векторное произведение 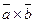в координатах записывается в виде:

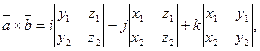
тогда скалярное произведение 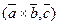в координатах имеет вид:

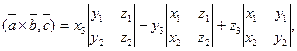
Правую часть последнего выражения можно записать с помощью определителя третьего порядка. Итак, смешанное произведение в координатах имеет следующий вид:

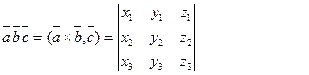
Свойства смешанного произведения векторов (проверьте самостоятельно):

1)

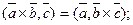
2)

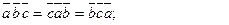
3) Пусть 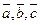- некомпланарные векторы.

Построим на этих векторах параллелепипед.

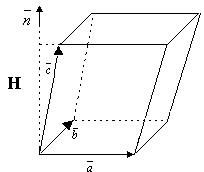
Смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на этих векторах.

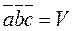
Действительно, 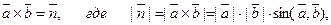то есть 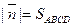, где S_ABCD - площадь основания.

Скалярное произведение 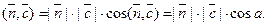Очевидно, что 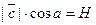, где H высота параллелепипеда.

Итак,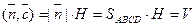

или, так как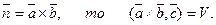

В частности, объем пирамиды, построенной на векторах 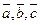равен

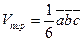
4) Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

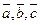- компланарные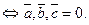

Пример 21. Показать, что заданные четыре точки лежат в одной

плоскости: А(2, 0, 1); В(-3, 1, 0); С(0,1, 3); D(-4, 3, 7).